1. 순수 굽힘과 전단력
우리가 처음 보의 굽힘 거동을 다룰 때 순수 굽힘(pure bending)을 알아본 적이 있다. 순수 굽힘 상태의 보는 모멘트에 의해서 휘고 보에 작용하는 전단력은 무시했다. 순수 굽힘은 외력 모멘트만 작용하는 상태이고 내력 모멘트가 휨이 발생하는 구간에서 일정(constant)하다는 것을 기억해야 한다. 보에 작용하는 외력이 모멘트뿐이니 전단력도 없고 따라서 전단 응력도 없다. 심심할 때 보에 모멘트를 주고 분할법으로 보의 내력 선도를 그려보자.
그런데 지금까지 외팔보에 외력 $P$를 작용하면 휜다는 예제를 많이 풀었으니 이게 무슨 소리인지 잠깐 어지러울 수 있다. 물론 전단력이 작용할 때도 당연히 보는 휘어지지만 이 때는 순수 굽힘이 아니다. 그렇다면 보에 전단력만이 작용할 때는 왜 휘어지는가? 이것은 전단력에 의해 내력 모멘트가 발생하기 때문이다. 이 전단력이 유발하는 내력 모멘트에 의해 보는 굽어지고 보에는 전단력이 작용하게 된다. 내력의 선도 글에서 다룬 보의 전단력과 모멘트를 다시 한번 생각해보자.
내력의 선도-분할법(Section Method)
1. 내력의 선도(Internal Force Diagram) 부재를 설계할 때 내력 선도를 그리는 것이 중요하다. 부재에 작용하는 힘과 모멘트를 한눈에 파악할 수 있고 하중이 집중되는 부분을 파악해 하중을 완화하
satlab.tistory.com



2. 보에 작용하는 전단 응력
아래 그림 4처럼 보에 임의의 전단 하중 q(x)가 작용한다고 하자.

그림 4에서 미소 길이 $dx$만 따내서 생각해보면 보에는 다음과 같이 내력 모멘트를 나타낼 수 있다. 이 $dx$는 하중이 작용하고 있지 않은 부분을 따내도 상관 없다.

그림 5에서 모멘트 증분 $dM$은 미소 길이 $dx$를 두고 모멘트가 차이 나는 것을 의미한다. 그림 2를 보면 거리에 따라 모멘트가 선형적으로 변하고 있는데 이것을 나타낸다고 생각하면 된다. 따라서 왼쪽 편과 오른쪽 편은 발생하는 수직 응력도 차이가 나게 된다. 다시 굽힘에 의한 응력을 생각해보자.
$$ \sigma_x = -\left(\frac{M}{I}\right)y $$
위 굽힘 응력에 식에 따라 모멘트가 차이가 있기 때문에 수직 응력도 마찬가지로 달라지게 된다. 중립축에서 거리 $y_0$만큼 떨어진 위치에서 다시 자유 물체도를 그려보자.

그림 6에서 $y_0$ 윗부분에 해당하는 영역에서 왼쪽 편과 오른쪽 편의 수직 응력은 각각 서로 다른 크기의 모멘트에 의해 발생했으므로 그 응력의 크기도 다르다. 따라서 양면에서 하중의 차이가 $dF_0$만큼 발생한다고 하면 아랫면에서 반대방향으로 $dF_0$와 같은 크기의 하중이 내력으로 발생해야 이 자유 물체도의 평형 상태를 만족하게 된다. 이것이 보에 작용하는 전단력의 크기가 된다. 이 층단면의 폭을 $b$라고 하면 전단력의 크기 $dF_0$는 다음과 같다.
$$ dF_0 = \tau bdx $$
이 거동은 우리가 두꺼운 책을 굽혀보면 쉽게 상상할 수 있다. 일단 책을 휘어보면 책의 각 낱장들이 서로 미끄러지며 책이 부드럽게 휘어지는 것을 관찰할 수 있다. 이것은 각 낱장들이 서로 미끄러짐(전단)에 저항하지 않기 때문에 크게 힘을 들이지 않고도 휘어질 수 있는 것이다. 만약 각 낱장에 풀을 발라서 붙여 놓는다면 낱장은 미끄러지지 못하므로 책을 굽히기는 더 어려워질 것이다. 다시 말해 낱장 사이사이마다 내력으로 전단력이 발생하여 책을 굽히려는 외력에 저항할 것이라고 상상할 수 있다. 이것이 보에 작용하는 전단력이다.
다시 그림 6의 양쪽 단면에 작용하는 수직 응력은 다음과 같다.
\begin{align} \sigma_x^{(1)} &= -\left(\frac{M}{I}\right)y \\\\ \sigma_x^{(2)} &= -\left(\frac{M+\frac{dM}{dx}dx}{I}\right)y \end{align}
축방향($x$)으로 힘의 평형을 생각하면 다음과 같다.
$$ \sum{F_x} = \int_{A_0}\sigma_x^{(1)}dA - \int_{A_0}\sigma_x^{(2)}dA + dF_0 = 0 $$
각 굽힘 응력을 대입하면 아래와 같다.
\begin{align} \sum{F_x} &= \int_{A_0}-\left(\frac{M}{I}\right)ydx - \int_{A_0}-\left(\frac{M+\frac{dM}{dx}dx}{I}\right)ydx + dF_0 \\\\ &= \int_{A_0}\left(\frac{\frac{dM}{dx}dx}{I}\right)ydx + dF_0 = 0 \end{align}
$$ \therefore \int_{A_0}\left(\frac{\frac{dM}{dx}dx}{I}\right)ydx + dF_0 = 0 $$
그런데 위 식에서 아래와 같이 이미 알고 있는 관계식을 적용하고 색칠된 면적 $A_0$의 중립축에 대한 1차 모멘트를 $Q$라고 하자.
$$ \frac{dM}{dx} = -V \\\\ dF_0 = \tau bdx \\\\ \int_{A_0}ydA = Q $$
대입하여 정리하면 다음과 같다.
\begin{align} &\left(\frac{\frac{dM}{dx}dx}{I}\right)\int_{A_0}ydx + \tau bdx = \frac{-Vdx}{I}Q + \tau bdx = 0 \end{align}
위 식에서 양변에서 $dx$를 소거하고 정리하면 다음과 같이 보에 작용하는 전단 응력을 구할 수 있다.
$$ \therefore \tau = \frac{VQ}{Ib} $$
여기에서 $Q$는 단면적 $A_0$의 중립축에 대한 1차 모멘트이고 다음과 같이 정의한다. $\bar{y_0}$는 단면적 $A_0$의 도심 위치이다.
$$ Q \equiv \int_{A_0} y dA = A_0\bar{y_0} $$
보의 축방향 단면에 발생하는 전단 응력의 방향은 전단력을 가정한 방향과 동일한 $\tau_{xy}$가 된다. 그리고 깊이 방향의 층 계면에 발생하는 전단 응력은 $tau_{yx}$가 된다. 이 두 성분은 공액 전단 응력으로 대칭이므로 같은 크기를 같는다.
$$ \tau = \tau_{xy} = \tau_{yx} $$


3. 어쩌라고
지금까지는 보에 작용하는 전단 응력을 계산할 때 아래처럼 단순히 평균 응력을 이용했다.
$$ \tau_{xy} = \frac{V}{A} $$
그러나 보에 작용하는 전단 응력은 보의 깊이에 따라 달라지며 다음과 같이 계산된다.
$$ \tau_{xy} = \frac{VQ}{Ib} $$
위 식에서 Q는 그림 6에서 처럼 보의 중립축에서 $y_0$만큼 떨어진 거리의 바깥 면적 $A_0$와 관련이 있다. 따라서 중립축에서 멀어질수록 $A_0$는 감소하여 $Q=0$이 되므로 가장 바깥면에서 전단 응력은 존재하지 않고 $Q$가 최대가 되는 지점은 보의 내부에 존재한다. 아래 예에서 보이겠지만 보의 단면에서 전단 응력은 포물선의 형태로 분포하며 최대 전단 응력은 평균 전단 응력보다 크다. 따라서 구조물을 설계할 때 굽힘을 받는 부재는 평균 전단 응력이 아닌 최대 전단 응력을 고려해서 설계할 필요가 있다.
4. 여러 가지 단면에서의 예
4.1. 외팔보
그림 9와 같은 외팔보가 있고 단면이 일정하다고 하자.

반력과 내력은 이미 다른 글에서 수차례 구했으니 결과만 쓰기로 한다.
\begin{align} A_x &= 0 \\\\ A_y &= P \\\\ M_A &= PL \\\\ F &= 0 \\\\ V &= -P \\\\ M &= P(x-L) \end{align}
이 보에 작용하는 수직 응력과 전단 응력은 다음과 같다.
\begin{align} \sigma_x &= -\left(\frac{M}{I}\right)y \\\\ \tau_{xy} &= \frac{VQ}{Ib} \end{align}
4.2. 사각형 단면
그림 9의 외팔보가 아래 그림 10과 같은 사각형 단면을 갖는 경우를 생각해 보자.

이 사각형 단면을 갖는 보의 특성치는 다음과 같다.
\begin{align} I &= I_z = \frac{bh^3}{12} \\\\ b &= \text{constant} \\\\ Q&= \int_{A_0} y dA \end{align}
먼저 $Q$를 구한다.
\begin{align} Q &= \int_{A_0} y dA \\\\ &= \int_{A_0} ybdy \\\\ &= \int_{y_0}^{h/2}bydy \\\\ &= b\int_{y_0}^{h/2}ydy \\\\ &= b\left[\frac{y^2}{2}\right]_{y_0}^{h/2} \\\\ &= \frac{b}{2}\left(\frac{h^2}{4}-y_0^2\right) \end{align}
$$ \therefore Q = \frac{b}{2}\left(\frac{h^2}{4}-y_0^2\right) $$
또는 다음과 같이 구할 수도 있다.
\begin{align} Q &= A_0\bar{y_0} \\\\ &= \left[b\left(\frac{h}{2}-y_0\right)\right] \times \left[\frac{1}{2}\left(\frac{h}{2}+y_0\right)\right] \\\\ &= \frac{b}{2}\left(\frac{h^2}{4}-y_0^2\right) \end{align}
따라서 전단 응력은 다음과 같다.
\begin{align} \tau &= \frac{VQ}{Ib} \\\\ &= \frac{V\cdot\frac{b}{2}\left(\frac{h^2}{4}-y_0^2\right)}{\frac{bh^3}{12}\cdot b} \\\\ &= \frac{6V}{bh^2}\left(\frac{h^2}{4}-y_0^2\right) \\\\ &= \frac{3}{2}\frac{V}{bh} \left[1-\left(\frac{2y_0}{h}\right)^2\right]\end{align}
그런데 단면의 면적 $A = bh$이므로,
$$ \therefore \tau = \frac{3}{2}\frac{V}{A} \left[1-\left(\frac{2y_0}{h}\right)^2\right] $$
위 식의 형태는 parabolic distribution이라는 것을 한눈에 알아챌 수 있다. 몇 가지 경우에 대해 전단 응력을 살펴보자. 먼저 $ y_0=\pm h/2 $인 경우 전단 응력 $\tau = 0$이 된다. 바깥면에서는 전단 응력이 존재하지 않는다. 그리고 $y_0=0$인 경우 전단 응력은 최댓값을 가지며 다음과 같다.
$$ \tau_{\text{max}} = \frac{3}{2}\frac{V}{A} $$
$$ \therefore \tau_{\text{max}} = \frac{3}{2}\tau_{\text{av}} $$
즉, 최대 전단 응력은 중립축에서 발생하며 평균 전단 응력의 1.5배가 된다.

4.3. 원형 단면
그림 9의 외팔보가 아래 그림 12와 같이 반경이 $c$인 원형 단면을 갖는 경우를 생각해 보자.
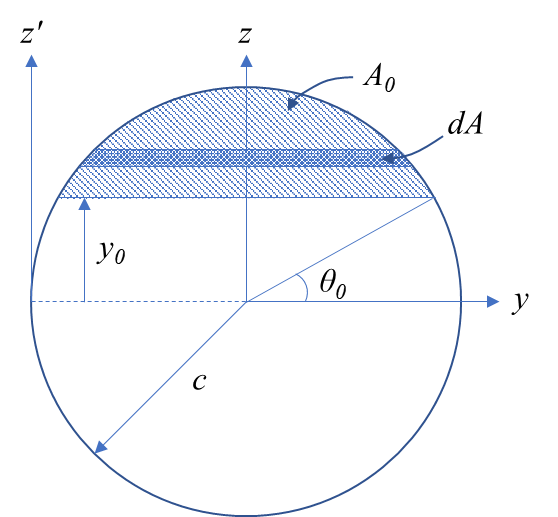
이 단면의 특성치는 다음과 같다.
\begin{align} I &= I_z = \frac{\pi}{4}c^4 \\\\ b(y_0) &= 2c\cos\theta_0 \\\\ Q&= \int_{A_0} y dA \end{align}
극좌표를 이용하기 위해 다음과 같이 관계식을 정리한다.
\begin{align} y &= c\sin\theta \\\\ z &= -c\cos\theta \\\\ dA &= 2|z|dy \\\\ &= 2c\cos\theta dy \end{align}
그런데 $dy = c\cos\theta d\theta$이므로,
$$ \therefore dA = 2c^2\cos^2\theta d\theta $$
적분을 이용해 $Q$를 구해보면 다음과 같다.
\begin{align} Q &= \int_{A_0} y dA \\\\ &= \int_{A_0} (c\sin\theta)(2c^2\cos^2\theta d\theta) \\\\ &= \int_{\theta_0}^{\pi/2} 2c^3\cos^2\theta\sin\theta d\theta \\\\ &= -2c^3\int_{\theta_0}^{\pi/2}\cos^2\theta(-\sin\theta)d\theta \\\\ &= -2c^3\left[ \frac{1}{3}\cos^3\theta \right]_{\theta_0}^{\pi/2} \\\\ &= \frac{2}{3}c^3\cos^3\theta_0 \end{align}
$$ \therefore Q = \frac{2}{3}c^3\cos^3\theta_0 $$
따라서 전단 응력은 다음과 같다.
\begin{align} \tau &= \frac{VQ}{Ib} \\\\ &= \frac{V\cdot\frac{2}{3}c^3\cos^3\theta_0}{\frac{\pi}{4}c^4\cdot 2c\cos\theta_0} \\\\ &= \frac{4V}{3\pi c^2}\cos^2\theta_0 \end{align}
그런데 단면의 면적 $A=\pi c^2$이고 $cos^2\theta_0$는 다음과 같이 쓸 수 있다.
\begin{align} \cos^2\theta_0 &= 1-\sin^2\theta_0 \\\\ &= 1-\left(\frac{y_0}{c}\right)^2 \end{align}
$$ \therefore \tau_{xy} = \frac{4}{3}\frac{V}{A}\left[1-\left(\frac{y_0}{c}\right)^2\right] $$
원형 단면의 전단 응력 역시 parabolic distribution임을 알 수 있다. 마찬가지로 몇 가지 경우에 대해 생각해보자. 먼저 $y_0=c$인 경우 $\tau =0$이 된다. 또 $y_0=0$인 경우 전단 응력은 최댓값이 되며 다음과 같다.
$$ \tau_{\text{max}} = \frac{4}{3}\frac{V}{A} $$
$$ \therefore \tau_{\text{max}} = \frac{4}{3}\tau_{\text{av}} $$
최대 전단 응력은 중립축에서 발생하며 평균 전단 응력의 1.33배가 된다. 분포는 그림 11과 같을 것이다.
5. 유효 전단 면적 (Effective Shear Area)
유효 전단 면적은 다음과 같이 정의한다.
$$ A_s = kA $$
여기에서 $k$는 다음과 같이 최대 전단 응력과 평균 전단 응력의 비를 나타낸다.
$$ k = \frac{\tau_{\text{av}}}{\tau_{\text{max}}} $$
실제 단면적이 $A$라고 하면 평균 전단 응력은 다음과 같다.
$$ \tau_{\text{av}} = \frac{V}{A} $$
위 식에서 실제 단면적 $A$ 대신 유효 전단 면적 $A_s$를 이용하여 계산하면 최대 전단 응력을 구할 수 있다.
$$ \tau_{\text{max}} = \frac{V}{A_s} = \frac{V}{kA}$$
사각형 단면에서 $k$값은 다음과 같다.
$$ k = \frac{\tau_{\text{av}}}{\tau_{\text{max}}} = \frac{2}{3} $$
원형 단면에서 $k$값은 다음과 같다.
$$ k = \frac{\tau_{\text{av}}}{\tau_{\text{max}}} = \frac{3}{4} $$
형강의 경우 유효 전단 면적은 아래 그림 13처럼 웹(web)의 면적으로 하지만 실제 계산은 아래 전단 응력 식을 그대로 이용한다.
$$ \tau = \frac{VQ}{Ib} $$





최근댓글