1. 내력의 선도(Internal Force Diagram)
부재를 설계할 때 내력 선도를 그리는 것이 중요하다. 부재에 작용하는 힘과 모멘트를 한눈에 파악할 수 있고 하중이 집중되는 부분을 파악해 하중을 완화하거나 구조를 보강할 수 있기 때문이다.
파악해야 할 내력의 선도에는 다음과 같은 것들이 있다.
AFD(Axial Force Diagram) - 축 하중 선도
SFD(Shear Force Diagram) - 전단 하중 선
BMD(Bending Moment Diagram) - 굽힘 모멘트 선도
우리가 지금까지 다룬 내력에는 수직력, 전단력, 그리고 내력 모멘트가 있으며 각각 AFD, SFD 그리고 BMD에 대응하는 내력들이다. 이런 내력 선도를 그리는 방법은 세 가지 정도가 있는데 분할법, 직접 적분법, 그리고 특이함수법이 있다. 고등학교 수학만 할 줄 알면 누구나 할 수 있는 것들이니 천천히 알아보자.
2. 분할법(Section Method)
분할법은 우리가 부재의 내력과 응력을 구하기 위해 지금까지 해오던 방법이다. 부재를 싹둑 잘라서 자유물체도(FBD, free body diagram)를 그리고 평형 방정식을 세우던 바로 그 방법이다. 따라서 늘 하던 대로 먼저 반력을 구하고, 내력을 구하고, 마지막 앞서 구한 내력을 그래프로 그리면 된다. 더 이상 자세한 설명은 생략한다.
2.1. 외팔보(Cantilever)
또 외팔보야? 하고 지겹게 생각할 수 있지만 오늘도 외팔보를 하는 거다.

그림 1에 자유단에 하중 $P$가 작용하는 외팔보를 나타냈다. 반력을 먼저 구하고 내력을 구할 건데 그림을 두 번 그리기는 귀찮으니까 가정한 반력을 미리 표시해 두었다. 먼저 반력을 구하기 위해 평형 방정식을 세워보자.
\begin{align} \sum{F_x} &= A_x = 0 \\\\ \sum{F_y} &= A_y - P = 0 \\\\ \sum{M_z}|_{x=0} &= M_A - PL = 0 \end{align}
\begin{align} \therefore A_x &= 0 \\\\ A_y &= P \\\\ M_A &= PL \end{align}
그동안 많이 해왔기 때문에 너무나 편안하고 안락하게 조금의 스트레스도 없이 반력을 구했다. 이제 내력을 구하기 위해 거리가 $x$가 되는 지점을 싹둑 자르고 내력을 가정해서 자유 물체도를 그려본다.

내력의 방향을 적절하게 잘 가정했다. 다시 강조하지만 면의 외향 벡터 방향에 맞춰서 내력을 가정하는 것이 중요하다.
\begin{align} \sum{F_x} &= A_x + F = 0 \\\\ \sum{F_y} &= A_y + V = 0 \\\\ \sum{M_z}|_{x=0} &= M_A + M + Vx = 0 \end{align}
\begin{align} \therefore F &= -A_x = 0 \\\\ V &= -A_y = -P \\\\ M &= -M_A - Vx = P(x-L) \end{align}
이제 위에 구한 내력을 그래프로 그리면 된다. 각각의 그래프를 그림 3부터 5에 나타냈다.


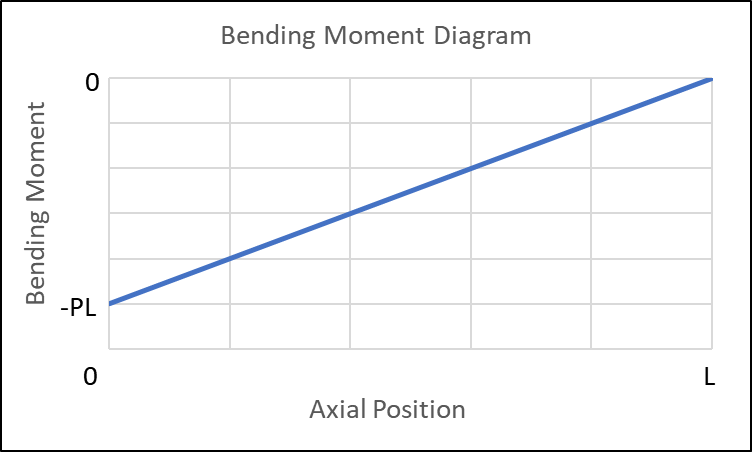
2.2. 집중 하중(Concentrated Load)
이제 외팔보는 너무 쉬우니까 단순보에 집중 하중이 작용하는 경우를 알아보자.

먼저 다음과 같이 반력을 구한다.
\begin{align} \sum{F_x} &= A_x = 0 \\\\ \sum{F_y} &= A_y +B_y - P = 0 \\\\ \sum{M_z}|_{x=0} &= B_yL -Pa = 0 \end{align}
\begin{align} \therefore &A_x = 0 \\\\ &A_y + B_y = P \\\\ &B_y = \frac{Pa}{L} \\\\ &A_y = P - B_y = P\left(1-\frac{a}{L}\right) = \frac{Pb}{L} \end{align}
내력을 구할 때는 하중 $P$가 작용하기 전과 후를 나누어서 따져 봐야 한다.
A. $ 0 \leqq x \leqq a $

\begin{align} \sum{F_x} &= A_x + F_1 = 0 \\\\ \sum{F_y} &= A_y + V_1 = 0 \\\\ \sum{M_z}|_{x=0} &= M_1 + V_1x = 0 \end{align}
\begin{align} \therefore F_1 &= -A_x = 0 \\\\ V_1 &= -A_y = -\frac{Pb}{L} \\\\ M_1 &= -V_1x = \frac{Pbx}{L} \end{align}
B. $ a \leqq x \leqq L $

\begin{align} \sum{F_x} &= A_x + F_2 = 0 \\\\ \sum{F_y} &= A_y - P + V_2 = 0 \\\\ \sum{M_z}|_{x=0} &= M_2 - Pa + V_2x = 0 \end{align}
\begin{align} \therefore F_2 &= -A_x = 0 \\\\ V_2 &= P - A_y = B_y = \frac{Pa}{L} \\\\ M_2 &= Pa -\frac{Pa}{L}x = Pa\left(1-\frac{x}{L}\right) \end{align}
위에서 구한 내력을 전체 구간에 대해 그래프로 그려보면 그림 8에서 10과 같이 나타난다.



2.3. 집중 모멘트(Concentrated Moment)

집중 모멘트가 작용하는 보를 생각해보자. 마찬가지로 자동으로 반력을 먼저 구해본다.
\begin{align} \sum{F_x} &= A_x = 0 \\\\ \sum{F_y} &= A_y +B_y = 0 \\\\ \sum{M_z}|_{x=0} &= B_yL + M_0 = 0 \end{align}
\begin{align} \therefore &A_x = 0 \\\\ &A_y + B_y = 0 \\\\ &B_y = -\frac{M_0}{L} \\\\ &A_y = -B_y = \frac{M_0}{L} \end{align}
마찬가지로 하중점 전후로 구간을 나눠서 자유물체도를 그리고 내력을 구한다.
A. $ 0 \leqq x \leqq a $

\begin{align} \sum{F_x} &= A_x + F_1 = 0 \\\\ \sum{F_y} &= A_y + V_1 = 0 \\\\ \sum{M_z}|_{x=0} &= M_1 + V_1x = 0 \end{align}
\begin{align} \therefore F_1 &= -A_x = 0 \\\\ V_1 &= -A_y = -\frac{M_0}{L} \\\\ M_1 &= -V_1x = \frac{M_0x}{L} \end{align}
B. $ a \leqq x \leqq L $

\begin{align} \sum{F_x} &= A_x + F_2 = 0 \\\\ \sum{F_y} &= A_y + V_2 = 0 \\\\ \sum{M_z}|_{x=0} &= M_0 + M_2 + V_2x = 0 \end{align}
\begin{align} \therefore F_2 &= -A_x = 0 \\\\ V_2 &= - A_y = -\frac{M_0}{L} \\\\ M_2 &= -M_0 + \frac{M_0x}{L} = -M_0\left(1-\frac{x}{L}\right) \end{align}
위에서 구한 내력을 전체 구간에 대해 그래프로 그려보면 그림 14에서 16과 같이 나타난다.







최근댓글