복합보의 굽힘 - 보강 콘크리트 보(Reinforced Concrete Beams)

목차

• 5. 보강 콘크리트 보 (Reinforced Concrete Beams)
  • 5.1. 이론적 방법
    • 5.1.1. 굽힘 변형률
    • 5.1.2. 굽힘 응력
    • 5.1.3. 굽힘 모멘트
    • 5.1.4. 중립축의 위치
    • 5.1.5. 곡률
    • 5.1.6. 굽힘 응력
  • 5.2. 변환 단면법
    • 5.2.1. 중립축의 위치
    • 5.2.2. 곡률
    • 5.2.3. 굽힘 응력

5. 보강 콘크리트 보 (Reinforced Concrete Beams)

 이번에는 보강된 콘크리트 보를 생각해 보자. 앞서 말했듯이 콘크리트는 인장이 취약하기 때문에 인장이 발생할 것으로 예상되는 부분에 철근을 삽입하기로 한다. 이를 아래 그림에 나타냈다. 중립축의 위치를 $k$를 이용해 나타냈다.

 

그림 1. 보강 콘크리트 보

 

 여기에서 $n$은 철근의 개수이고 $d$는 철근의 지름이다. 따라서 철근의 단면적 $A_s$와 콘크리트의 단면적 $A_c$는 다음과 같다.

$$\begin{align} A_s &= n\cdot\frac{pi}{4}d^2 \\\\ A_c &= bh \end{align}$$

 

 단면적의 아랫첨자를 그대로 써서 철근의 영률을 $E_s$, 그리고 콘크리트의 영률을 $E_c$라고 한다.

 

 중요한 가정은 모든 인장력은 철근이 부담한다는 것이다. 마찬가지로 모든 압축력은 콘크리트가 부담하는 것으로 본다. 따라서 보강 콘크리트 보는 앞서 다룬 인장과 압축의 영률이 다른 경우와 같다.

 

그림 2. 보강 콘크리트 보의 인장과 압축

 

5.1. 이론적 방법

5.1.1. 굽힘 변형률

 여러 번 말해서 피곤하겠지만 변형이 작은 오일러 빔이라고 보면 곡률은 일정하다고 가정하므로 변형률은 연속이며 다음과 같다.

$$\varepsilon_x = -\frac{y}{\rho}$$

 

5.1.2. 굽힘 응력

 콘크리트에 발생하는 최대 압축 응력은 다음과 같다.

$$\begin{align} \sigma_c &= E_c\left(-\frac{y}{\rho}\right)|_{y=kh} \\\\ &= -\frac{E_c}{\rho}kh \end{align}$$

 

 철근에 발생하는 최대 인장 응력은 다음과 같다.

$$\begin{align} \sigma_s &= E_s\left(-\frac{y}{\rho}\right)|_{y=(1-k)h} \\\\ &= -\frac{E_s}{\rho}(1-k)h \end{align}$$

 

5.1.3. 굽힘 모멘트

 굽힘 모멘트는 항상 구하던 대로 구하면 된다. 다만 철근에는 깊이에 상관없이 항상 최대 응력이 작용하는 것으로 계산하면 복잡한 단면에 대한 적분을 쉽게 다를 수 있고 좀 더 보수적으로 다루는 효과가 있다.

$$\begin{align} M &= \int_A \sigma_x(-y)dA \\\\ &= \int_{A_c} \sigma_x^c(-y)dA + \int_{A_t} \sigma_x^s(-y)dA \\\\ &= int_0^{kh} \left(-\frac{E_c}{\rho}y\right)(-y)bdy + \sigma_s(1-k)h\cdot A_s \end{align}$$

 

 여기에 위에서 구한 응력을 대입하면,

$$\begin{align} M &= \frac{bE_c}{\rho}\int_0^{kh} y^2dy + \frac{E_s}{\rho}(1-k)^2h^2A_s \\\\ &= \frac{bE_c}{\rho}\left[\frac{1}{3}y^3\right]_{0}^{kh} + \frac{E_s}{\rho}(1-k)^2h^2A_s \\\\ &= \frac{h^2}{\rho}\left[\frac{1}{3}E_cA_ck^3 + E_sA_s(1-k)^2\right] \end{align}$$

 

 따라서 곡률은 다음과 같다.

$$\therefore \kappa = \frac{1}{\rho} = \frac{M}{h^2\left[\frac{1}{3}E_cA_ck^3 + E_sA_s(1-k)^2\right]}$$

 

5.1.4. 중립축의 위치

 위에서 하던 것처럼 중립축의 위치를 구하기 위해 단면에 작용하는 수직력의 합이 0이라는 조건을 이용한다.

$$\begin{align} F &= \int_A \sigma_x dA = \int_{A_c} \sigma_x^c dA + \int_{A_s} \sigma_x^s dA \\\\ &= \int_0^{kh}\left(-\frac{E_c}{\rho}y\right)(bdy) + \sigma_sA_s \end{align}$$

 

 철근의 응력을 최대 응력으로 취급하고 정리해 보자.

$$\begin{align} F &= -\frac{b}{\rho}E_c\left[\frac{y^2}{2}\right]_0^{kh} + \frac{E_s}{\rho}(1-k)hA_s \\\\ &= -\frac{1}{\rho}\left[E_c\cdot b\cdot \frac{k^2h^2}{2} - E_s(1-k)hA_s\right] \\\\ &= 0 \end{align}$$

 

 다시 정리하면 다음과 같다.

$$E_c(bh)k^2 - 2E_sA_s(1-k) = 0$$

 

 위 식에서 $bh=A_c$이므로 중립축을 결정하는 식은 다음과 같이 쓸 수 있다.

$$\therefore E_cA_ck^2 - 2E_sA_s(1-k) = 0$$

 

 위 식은 $k$에 대한 2차 방정식이다. 식의 양변을 $E_cA_c$로 나누고 정리하면 다음과 같이 쓸 수 있다.

$$k^2 - 2p(1-k) = 0$$

 

 한 번 더 전개하면,

$$k^2 +2pk -2p = 0$$

 

 위 식을 근의 공식을 이용해 풀면 $k$를 구할 수 있다.

$$k = -p \pm \sqrt{p^2+2p}$$

 

 그런데 $k>0$이므로 중립축의 위치를 결정하는 비율 $k$는 다음과 같이 결정된다.

$$\therefore k = -p + \sqrt{p^2 +2p}$$

 

 이때 $p$는 축방향 강성비(axial rigidity ratio)가 된다.

$$p = \frac{E_sA_s}{E_cA_c}$$

 

5.1.5. 곡률

 앞서 곡률을 이미 구했다.

$$\kappa = \frac{1}{\rho} = \frac{M}{h^2\left[\frac{1}{3}E_cA_ck^3 + E_sA_s(1-k)^2\right]}$$

 

 중립축의 위치를 결정하는 식은 다음과 같이 구했다.

$$E_cA_ck^2 - 2E_sA_s(1-k) = 0$$

 

 이 식을 곡률 식에 대입하여 콘크리트에 대한 영률로 정리하면 다음과 같다.

$$\begin{align} \kappa &= \frac{1}{\rho} \\\\ &= \frac{M}{h^2\left[\frac{1}{3}E_cA_ck^3 + E_sA_s(1-k)^2\right]} \\\\ &= \frac{M}{h^2\left[\frac{1}{3}E_cA_ck^3 + \frac{1}{2}E_cA_ck^2(1-k)\right]} \end{align}$$

 

$$\therefore \kappa = \frac{1}{\rho} = \frac{2M}{k^2h^2E_cA_c\left(1-\frac{k}{3}\right)}$$

 

5.1.6. 굽힘 응력

 앞서 나타낸 굽힘 응력 식에 곡률을 대입하여 콘크리트와 철근에 작용하는 최대 응력을 구한다.

$$\begin{align} \sigma_c &= -\frac{E_c}{\rho}kh \\\\ &= -E_ckh \cdot \frac{2M}{k^2h^2E_cA_c\left(1-\frac{k}{3}\right)} \\\\ &= -\frac{2M}{khA_c\left(1-\frac{k}{3}\right)} \\\\ \sigma_s &= \frac{E_s}{\rho}(1-k)h \\\\ &= E_s(1-k)h\left(\frac{2M}{k^2h^2E_cA_c\left(1-\frac{k}{3}\right)}\right) \\\\ &= \frac{M}{A_sh\left(1-\frac{k}{3}\right)} \end{align}$$

 

5.2. 변환 단면법

 변환 단면법으로 보강 콘크리트 문제를 다룰 수도 있다. 이 때는 아래 그림처럼 인장 응력이 발생하는 부위에는 철근만 있다고 생각하며 된다. 어차피 모든 인장력은 철근이 부담한다고 생각하기 때문이다.

 

그림 3. 보강 콘크리트 보의 가정

 

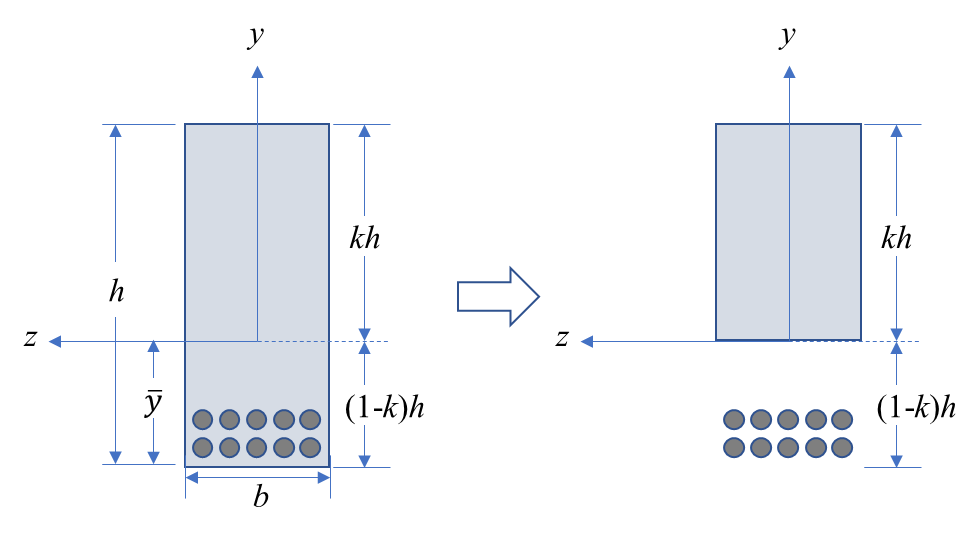
 변환된 단면은 아래 그림처럼 개략적으로 나타낼 수 있다.

$$b' = \frac{E_c}{E_s}b$$

 

그림 4. 보강 콘크리트보의 간략화

 

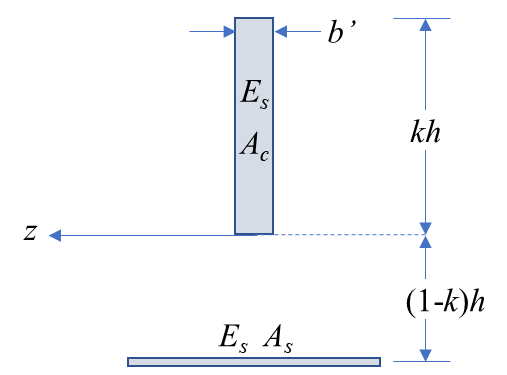
5.2.1. 중립축의 위치

 중립축의 위치는 모멘트 평형으로 다음과 같이 구한다.

$$(b'kh)\left(\frac{1}{2}kh\right) = A_s[(1-k)h]$$

 

 변환면 치수 $b'$을 $b$로 나타내면 다음과 같다.

$$b' = \frac{E_c}{E_s}b$$

 

 이 것을 대입하고 양변을 정리하면 다음과 같이 $k$에 대한 이차방정식을 얻을 수 있다.

$$k^2 - 2\frac{E_sA_s}{E_cA_c}(1-k) = 0$$

 

 앞서 구한 바와 같이 중립축의 위치 $k$를 결정할 수 있다.

$$\therefore k = -p + \sqrt{p^2 +2p}$$

$$p = \frac{E_sA_s}{E_cA_c}$$

 

5.2.2. 곡률

 곡률은 다음과 같다.

$$\kappa = \frac{1}{\rho} = \frac{M}{E_sI}$$

 

 단면의 2차 모멘트는 평행축 정리를 이용해 다음과 같이 구한다.

$$\begin{align} I &= \frac{b'}{12}(kh)^3 + (b'kh)\left(\frac{kh}{2}\right)^2 + A_s[(1-k)h]^2 \\\\ &= \frac{b'}{3}k^3h^3 + A_s(1-k)^2h^2 \\\\ &= \frac{E_c}{3E_s}bk^3h^3 + A_s(1-k)^2h^2 \end{align}$$

 

 따라서 곡률은 다음과 같이 정리된다.

$$\begin{align} \therefore \kappa = \frac{1}{\rho} &= \frac{2M}{k^2h^2E_cA_c\left(1-\frac{k}{3}\right)} \\\\ &= \frac{M}{h^2\left[\frac{1}{3}E_cA_ck^3 + E_sA_s(1-k)^2\right]} \end{align}$$

 

 위에서 이론적으로 구한 식과 동일한 것을 알 수 있다. 마찬가지로 중립축을 결정하는 식을 이용해 콘크리트에 대한 영률과 단면적만으로 나타내면 다음과 같이 정리할 수 있다.

$$\therefore \kappa = \frac{1}{\rho} = \frac{2M}{k^2h^2E_cA_c\left(1-\frac{k}{3}\right)}$$

 

5.2.3. 굽힘 응력

 굽힘 응력은 앞서 구한 것과 마찬가지 방법으로 구한다.

$$\begin{align} \sigma_c &= -\frac{E_c}{\rho}kh \\\\ \sigma_s &= \frac{E_s}{\rho}(1-k)h \end{align}$$