목차
1. 복합보 (Composite Beams)
복합보는 단면이 두 가지 이상의 재료로 구성된 보를 말한다. 지금까지는 단일 재료로 구성된 보만을 다뤘으나 실제로는 재료의 단점을 보완하기 위해 여러 재료로 구성된 복합보를 이용하는 경우가 종종 있다. 복합보를 다루는 방법으로는 이론적인 방법과 변환 단면법(transformed section method) 등이 있다.

대표적인 예가 요즘 부실 시공으로 논란인 철근 콘크리트이다. 심심하니까 철근 콘크리트에 대해 살짝 알아보자. 콘크리트는 단단한 바위를 시공 현장에서 설계자의 요구대로 성형할 수 있다는 장점이 있어 고대 로마시대부터 꾸준히 쓰여온 재료이다. 다만 콘크리트는 기본적으로 취성재이기 때문에 압축에는 아주 강하지만 인장에는 취약하다는 단점이 있다. 이것을 알고 있던 매우 똑똑한 고대 사람들은 콘크리트 건물이 압축 하중만을 받도록 돔(dome)이나 원호(arch) 형태로 설계했다. 로마에 가서 오래된 다리나 건물 출입구 구조를 보면 원호(아치, arch) 형태로 되어 있고 맨 위에 사다리 꼴 모양의 키스톤(key stone)을 박아서 압축 하중의 균형을 완성했다.


가장 오래된 콘크리트 건축물은 로마에 있는 판테온(Pantheon)이다. 판테온은 모든 신들을 위한 신전으로 기원전 27년 아우구스투스 황제 시절 집정관이었던 아그리파가 건축했다. 아그리파가 누구냐면 미술 공부하시는 분들이 데생 연습할 때 그리는 잘생긴 석고상 모델이 되시겠다. 어쨌거나 저쨌거나 판테온은 이후 80년 대화재 때 한 번 불타고 125년에 히드리아누스 황제가 재건했다. 그때 재건한 게 지금까지 쭈욱 내려오면서 현존하는 가장 오래된 콘크리트 건축물이 되었다. 판테온에 실제로 가보면 마치 얼마 전에 지은 것 같은 완벽한 보존 상태를 자랑하고 내부에 들어가 보면 격벽 없이 뻥 뚫린 공간이 나오며 돔형 천장으로 되어 있다. 이 건축물이 철근 없이 콘크리트만으로 지은 2000년 된 건축물이라는 걸 곱씹으면서 둘러보면 감탄이 나오게 된다. 로마에서 가볼 만한 무료 유적지 중 하나이지만 한국인들은 별로 찾지 않는 것 같다. 대부분 슥 들어갔다가 썰렁함에 별 감흥 없이 발길을 돌리는 것 같지만 우리는 이제 의미를 알았으니 로마에 가게 되면 꼭 방문해 보자.


누군가는 '아니 우리는 철근 좀 뺐다고 짓다가 무너지는데 로마 시대 콘크리트 건축물은 철근도 없이 2000년을 가다니!!' 라고 할 수도 있다. 사실 철근 콘크리트는 고층 건물을 지을 수 있는 아주 좋은 재료이지만 내부의 철근은 부식이 서서히 진행되기 때문에 수명을 대충 100년 내외로 본다. 그러나 저층 건물을 콘크리트만 이용해 잘 설계해서 지으면 천년을 갈 수가 있다. 그렇다고 땅값 비싼 서울에서 고층 건물을 포기할 수가 없지. 50년 뒤에는 재건축하자고 누우면 된다. 따라서 철근 콘크리트는 현대 건축에서 빼놓을 수 없는 필수 재료가 된 것이다. 방금은 농담으로 한 말이고 공학의 기본 철학은 경제성에 있다는 것을 잊어서는 안 된다. 요즘 공학자의 길을 걸으면서 과학자 흉내를 내려는 사람들이 있는데 잘못된 생각이다. 아무튼 1800년대 사람들이 콘크리트에 철사를 넣을 생각을 시작한 것 같다. 흙을 구워 만드는 화분에 철망을 넣는 것에서 시작해 독일과 미국에서 철근 콘크리트 공법으로 발전되었다. 인류가 많이 사용하는 철과 시멘트는 우연의 일치인지 열팽창 계수가 거의 같다. 따라서 온도가 오르락내리락해도 열변형이 비슷하므로 안정적이다. 또한 비싼 형강에 비해 저렴한 철근과 콘크리트를 혼합하면 더욱 경제적이라는 장점이 있다. 특히 강재는 콘크리트에 비해 인장 강도가 매우 높기 때문에 모든 인장력을 철근이 다 버틴다고 봐도 무방하다. 압축은 콘크리트가 받아줄 것이다. 자세한 것은 차차 알아보자.
2. 이론적 방법 (Theoritical Method)
이론적인 방법은 단지 우리가 지금까지 해왔대로 오일러 보의 가정을 이용해 곧이곧대로 계산하는 방법이다. 요즘 인기 있는 박막 분야에서도 이것을 이축 응력(biaxial stress) 상태로 확장하기만 하면 유명한 Stoney equaition을 얻을 수 있으니 봐두면 좋다.
2.1. 굽힘 변형률 (Bending Strain)
복합보도 변형이 작을 경우 오일러 보(Euler beam)이라고 볼 수 있다. 따라서 곡률이 일정하고 굽힘 변형률은 연속이다.
εx=−yρ
2.2. 굽힘 응력 (Bending Stress)
그림 1과 같이 단면의 영역마다 영률이 다르므로 굽힘 응력은 달라진다.
σ(1)x=E1εx=−E1ρyσ(2)x=E2εx=−E2ρy
2.3. 굽힘 모멘트 (Bending Moment)
굽힘 모멘트는 다음과 같이 적분으로 구한다.
M=∫Aσx(−y)dA
위 굽힘 응력과 굽힘 모멘트 식을 이용해 복합보의 굽힘 모멘트를 구하면 다음과 같다.
M=∫A1σ(1)x(−y)dA+∫A2σ(2)x(−y)dA=∫A1(−E1ρy)(−y)dA+∫A2(−E2ρy)(−y)dA=E1ρ∫A1y2dA+E2ρ∫A2y2dA=E1I1ρ+E2I2ρ
∴
2.4. 굽힘 응력 공식 (Bending Stress Formula)
다시 위의 굽힘 응력에 복합보의 곡률을 대입하면 다음과 같이 각 영역의 응력을 얻을 수 있다.
\begin{align} \sigma_x^{(1)} &= -\frac{E_1}{\rho}y = -\frac{ME_1}{E_1I_1 + E_2I_2}y \\\\ \sigma_x^{(2)} &= -\frac{E_2}{\rho}y = -\frac{ME_2}{E_1I_1 + E_2I_2}y \end{align}
2.5. 중립축의 위치 (Neutral Axis)
보의 단면에 작용하는 내력은 인장과 압축에 대해 평형 상태이다.
F = \int_A \sigma_xdA = 0
위 식에 복합보의 응력 상태를 적용하면 다음과 같이 전개된다.
\begin{align} \int_A \sigma_xdA &= \int_{A_1} \sigma_x^{(1)}dA + \int_{A_2} \sigma_x^{(2)}dA \\\\ &= \int_{A_1}\left(-\frac{E_1}{\rho}y\right)dA + \int_{A_2}\left(-\frac{E_2}{\rho}y\right)dA \\\\ &= -\frac{E_1}{\rho}\int_{A_1}ydA -\frac{E_2}{\rho}\int_{A_2}ydA \\\\ &= -\frac{E_1}{\rho}A_1\overline{y_1} - \frac{E_2}{\rho}A_2\overline{y_2} \\\\ &= -\frac{1}{\rho}(E_1A_1\overline{y_1} + E_2A_2\overline{y_2}) = 0 \end{align}
위 식에서 곡률은 상수이므로 중립축의 위치는 다음과 같이 결정된다.
\therefore E_1A_1\overline{y_1} + E_2A_2\overline{y_2} = 0
그래서 중립축은 어디야?라고 생각할 수 있는데 여기에서 \overline{y_i}는 중립축에서 떨어진 위치를 의미한다. 우리는 각 영역의 도심 위치를 형상 정보만 가지고도 알 수 있으므로 이를 이용해 중립축의 위치를 구할 수 있다.
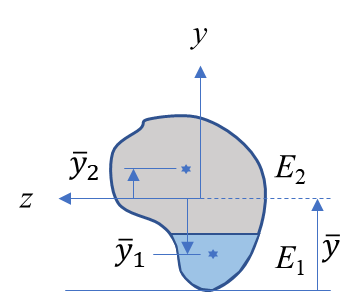
2.6. 사각형 단면의 예
심심하니까 사각형 단면에 대한 계산을 해보자. 먼저 중립축의 위치를 결정할 필요가 있다. 가장 아래쪽면을 기준으로 생각하면 아래 그림처럼 중립축을 나타낼 수 있다.
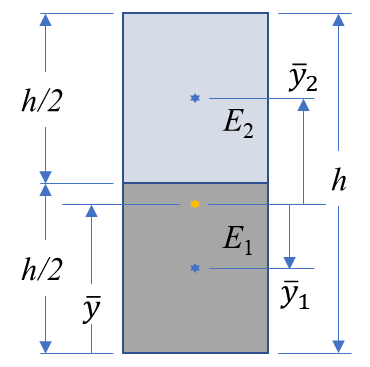
다음 식으로 중립축의 위치를 결정한다.
E_1A_1\overline{y_1} + E_2A_2\overline{y_2} = 0
여기에서 각 항은 다음과 같이 계산할 수 있다.
\begin{align} A_1 &= A_2 = \frac{bh}{2} \\\\ \overline{y_1} &= -\left(\overline{y}-\frac{h}{4}\right) \\\\ \overline{y_2} &= \left(h - \frac{h}{4}\right) - \overline{y} \\\\ &= \frac{3h}{4}-\overline{y} \end{align}
이 것들을 중립축의 위치를 결정하는 식에 대입하면 다음과 같이 정리할 수 있다.
E_1\left(\frac{bh}{2}\right)\left(\frac{h}{4}-\overline{y}\right) + E_2\left(\frac{bh}{2}\right)\left(\frac{3h}{4}-\overline{y}\right) = 0
위 식에서 bh/2를 없애고 정리하면 다음과 같다.
\begin{align} (E_1+E_2)\overline{y} &= E_1\frac{h}{4} + E_2\frac{3h}{4} \\\\ &= \frac{h}{4}(E_1 + 3E_2) \end{align}
\therefore \overline{y} = \frac{h(E_1+3E_2)}{4(E_1+E_2)}
만약 E_1 = 2E_2 라고 하면 하면 중립축의 위치는 아래와 같다.
\overline{y} = \frac{h}{4}\frac{5E_2}{3E_2} = \frac{5}{12}h
각 영역에 대한 단면의 2차 관성 모멘트는 다음과 같다.
\begin{align} I_1 &= \frac{b}{12}\left(\frac{h}{2}\right)^3 + A_1\overline{y_1}^2 \\\\ I_2 &= \frac{b}{12}\left(\frac{h}{2}\right)^3 + A_2\overline{y_2}^2 \end{align}
굽힘 응력은 다음과 같다.
\begin{align} \sigma_x^{(1)} &= -\frac{E_1M}{E_1I_1 + E_2I_2}y \\\\ \sigma_x^{(2)} &= -\frac{E_2M}{E_1I_1+E_2I_2}y \end{align}
3. 인장과 압축에 대한 영률이 다른 경우
보통 인장과 압축의 영률이 같다고 가정하고 재료를 취급하는 경우가 많지만 그렇지 않은 경우들이 종종 있다. 세라믹(ceramics)과 같은 취성재들이 특히 그렇고 뼈(bone)와 같은 다공성 재료(porous media)가 그렇다. 여기에 더해 섬유강화(fiber reinforced) 재료들도 이런 특성을 보일 수 있는데 대표적인 예가 철근 콘크리트이다.
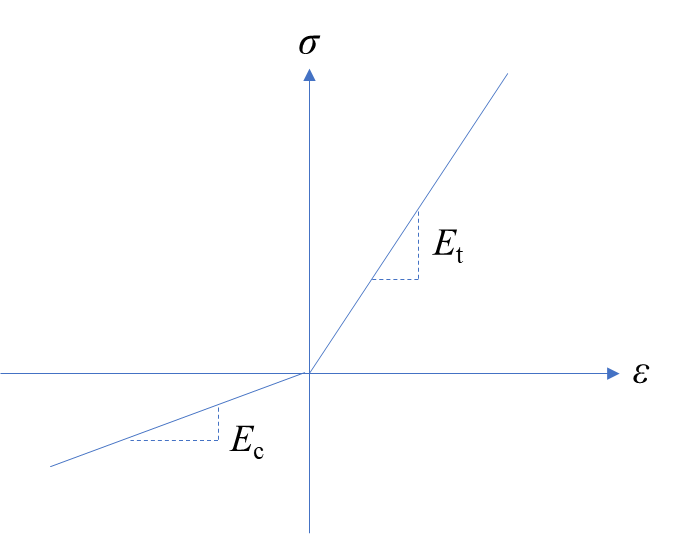
어쨌거나 저쨌거나 이런 경우에도 쫄지 말고 애초에 영률이 다른 두 재료로 구성된 복합보로 취급하면 된다. 다만 중립축의 위치가 두 재료의 계면(interface)이 될 뿐이다.
먼저 중립축의 위치를 결정한다.
E_cA_c\overline{y_c} + E_tA_t\overline{y_t} = 0
굽힘 응력은 다음과 같다.
\begin{align} \sigma_x^{c} &= -\frac{E_c}{\rho}y = -\frac{ME_c}{E_cI_c + E_tI_t}y \\\\ \sigma_x^{t} &= -\frac{E_t}{\rho}y = -\frac{ME_t}{E_cI_c + E_tI_t}y \end{align}
3.1. 사각형 단면의 예
아래 그림에 인장과 압축 특성이 다른 재료로 이루어진 보의 단면을 나타냈다.
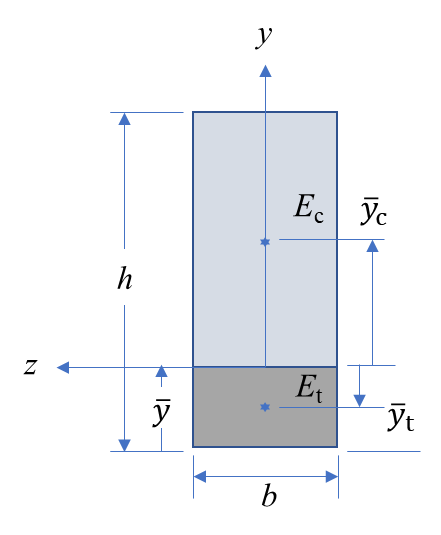
위 그림에서 확인할 수 있듯 중립축을 경계로 아래는 인장 위는 압축이므로 영률로 중립축을 기준으로 서로 다르다. 먼저 중립축은 다음 식으로 결정한다.
E_cA_c\overline{y_c} + E_tA_t\overline{y_t} = 0
위 식에서 각 영역의 단면적과 도심 위치는 다음과 같다.
\begin{align} A_c &= b(h-\overline{y}) \\\\ A_t &= b\overline{y} \\\\ \overline{y_c} &= -\frac{\overline{y}}{2} \\\\ \overline{y_t} &= \frac{1}{2}(h-\overline{y}) \end{align}
이 값들을 대입하면 다음 식을 얻고 \overline{y}에 대해 풀면 중립축의 위치를 구할 수 있다.
E_cb(h-\overline{y})\left(-\frac{\overline{y}}{2}\right) + E_tb\overline{y}\cdot\frac{1}{2}(h-\overline{y}) = 0
각 영역의 단면 2차 모멘트는 평행축 정리를 이용하여 구하면 된다.
\begin{align} I_c &= \frac{b}{12}\overline{y}^3 + A_c\overline{y_c}^2 \\\\ I_t &= \frac{b}{12}(h-\overline{y})^3 + A_t\overline{y_t}^2 \end{align}




최근댓글