소성 굽힘 (Plastic Bending)

1. 소성이 발생한 보
2. 재료와 경도
3. 탄소성 굽힘
4. 잔류 응력

1. 소성이 발생한 보

굽힘 하중을 받는 보의 변형이 탄성 영역에 있을 때는 아래와 같은 수직 응력과 굽힘 모멘트 사이의 관계를 이용했다.

$\sigma_x = -\frac{M}{I}y$

이제부터는 보에 큰 굽힘 하중이 작용하여 소성이 발생하는 경우를 생각해 보자. 위 식을 보면 보가 굽힘 하중을 받을 때 최대 응력이 발생하는 부분은 가장 바깥쪽이다. 만약 응력이 항복 강도에 도달하게 되면 가장 바깥쪽부터 소성이 발생하기 시작하고 하중이 커질수록 점차 내부로 소성 영역이 전파할 것이라는 것을 짐작할 수 있다.

2. 재료와 경도

일반적인 탄소성 재료는 대체로 탄성 구간 이후에 응력 변형률 선도가 완만하게 증가한다. 이 구간에서 제하(unloading)를 하면 탄성구간의 기울기를 따르면서 변형이 회복되므로 영구 변형이 남는다. 이 상태에서 다시 하중을 인가(loading)하면 다시 초기 탄성 구간을 따르게 된다. 이렇게 재료는 초기 탄성구간의 기울기를 따르면서 응력이 증가하다가 제하 시점의 응력에 도달하면 원래의 응력 변형률 선도를 따르게 된다. 따라서 이 제하 시점의 응력이 새로운 항복강도가 된다. 이렇게 소성 변형 이후 항복 강도가 증가하는 현상을 변형률 경화 현상(strain hardening effect)이라고 한다.

그런데 우리가 어떤 재료를 만났을 때 이 재료의 하중 이력을 알지 못한다. 따라서 영구 변형이 남은 상태를 초기 상태로 생각하게 될 것이다. 이런 경우에는 그림 2처럼 항복 강도가 더 큰 새로운 재료인 것처럼 생각할 수가 있다. 이렇게 같은 원소재를 이용하더라도 가공경화나 열처리를 통해 강도를 의도적으로 증가시킬 수 있다. 그러나 연신률이 저하되는 것은 받아들여야 할 것이다. 아무래도 세상에 모든 것을 얻는 경우는 없는 듯하다.

그림 3과 같은 완전 탄소성 재료는 항복 이후 기울기가 0이므로 제하 후 다시 하중을 재인가하더라도 항복강도가 변하지 않는다. 다시 말해 완전 탄소성 재료는 변형률 경화 현상이 없는 것이다. 단축 인장 상태에 있는 완전 탄소성 재료에 소성 변형이 발생하면 더 이상 외력에 저항하지 못한다. 왜냐하면 단면의 모든 영역에서 응력의 크기가 동일해 재료 전체가 일시에 소성 상태가 되기 때문이다.

그러나 비틀림이나 굽힘은 모든 면적이 소성 상태가 되는 것이 아니고 재료의 바깥부터 소성 상태가 전파하기 때문에 모든 단면이 소성 상태에 빠지기 전까지는 계속해서 저항할 수 있다. 이전 소성 변형에 대해 다룬 글에서도 다뤘으니 찾아보자. 그러나 굽힘에서도 모든 단면이 소성 상태에 빠지면 더이상 굽힘 하중에 저항할 수 없으며 이때부터는 건드리는 대로 휙휙 돌아가는 경첩(hinge)과 같은 거동을 한다. 이것을 소성 힌지(plastic hinge)라고 한다. 유한요소해석에서 재료 모델을 적용할 때 편의상 이런 완전 탄소성 재료를 이용하는 경우가 많다. 따라서 구조물이 소성 힌지 상태에 빠져 실제와 다른 거동을 하지 않는지 주의할 필요가 있다.

여기서 잠시 경도(hardness)를 생각해 보자. 먼저 '경하다'는 것은 무엇을 의미할까? 학교에서 경도를 배우지만 사실 대충 배우고 넘어간다. 보통 강도를 더 중요하게 다루고 응력이나 변형률을 설명하기 바쁘기 때문이다. 결론부터 말하자면 경도는 우리가 관심 있는 재료를 찍어 눌렀을 때(indentation) 찍힌 흔적(dent)이 잘 남느냐 안 남느냐를 따지는 것이다. 이때 다른 재료가 무엇이냐에 따라 흔적이 남는 정도가 달라지므로 상대적인 값이 되고 상대물의 형상에 뾰족하면 더 흔적이 잘 남게 되므로 압입자(indenter)의 형상에 따라 결과다 달라질 수 있다. 따라서 여러 가지 경도 시험법이 존재하며 때때로 우리를 피곤하게 한다.

어쨌거나 저쨌거나 찍힌 흔적이 남는다는 것은 영구 변형이 발생했다는 뜻이다. 그런데 재료가 변형률 경화를 겪으며 점점 항복강도가 커지면 같은 하중으로 눌러도 눌린 흔적이 점점 작게 될 것이다. 다시 말해 경도는 소성 변형의 이력과도 관련이 있는 것이다.

3. 탄소성 굽힘

3.1. 탄소성 굽힘 상태

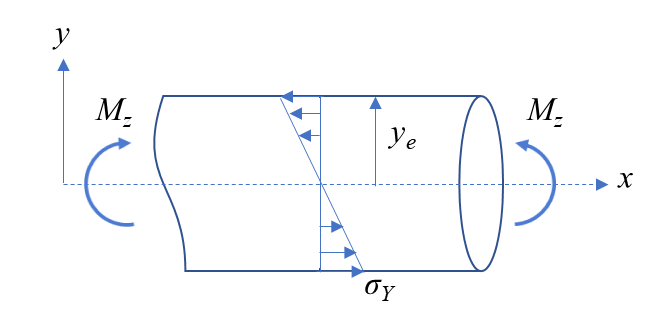
재료가 굽어질 때 소성이 발생하게 되면 굽힘 하중이 커짐에 따라 그림 1처럼 가장 바깥 부분부터 소성 영역이 전파하게 된다. 이 상태의 단면을 그림 2에 나타냈다. 도심에서 $y_e$ 거리만큼은 아직 탄성 상태이다. $A_c$ 는 압축 상태의 면적을 의미하고 $A_t$ 는 인장 상태의 면적을 의미한다.

3.2. 굽힘 변형률

굽힘 응력은 소성이 발생하면 증가를 멈추지만 변형률은 완전 탄성체와 마찬가지로 연속적으로 증가한다.

$\varepsilon_x = -\frac{y}{\rho}$

소성이 시작되는 깊이는 $y_e$ 가 되고 이 깊이의 변형률이 항복이 막 시작되는 변형률이다.

$\begin{align} \varepsilon_Y &= \varepsilon_x|_{y_e} \\\\ &= -\left( -\frac{y_e}{\rho} \right) \\\\ &= \frac{y_e}{\rho} \end{align}$

곡률은 다음과 같이 소성 변형률로 나타낼 수 있다.

$\kappa = \frac{1}{\rho} = \frac{\varepsilon_Y}{y_e}$

위 두 식을 이용하면 소성 이후의 굽힘 변형률은 다음과 같다.

$\epsilon_x = -\frac{y}{\rho} = -\frac{y}{y_e}\varepsilon_Y$

3.3 굽힘 응력

내부의 탄성 영역은 도심에서 $y_e$ 만큼 떨어진 영역 내부이다.

$-y_e \leq y \leq y_e$

이 탄성 영역에서의 응력은 다음과 같다.

$\begin{align} \sigma_x &= E\varepsilon_x \\\\ &= E\left(-\frac{y}{y_e}\varepsilon_Y\right) \\\\ &= -\frac{y}{y_e}(E\varepsilon_Y) \end{align}$

위 식에서 $E\epsilon_Y = \sigma_Y$ 가 되므로 응력은 다음과 같이 쓸 수 있다.

$\sigma_x = -\frac{y}{y_e}\sigma_Y$

인장 상태의 소성 영역은 도심에서 $-y_e$ 떨어진 영역부터 하단 표면까지가 된다. 완전 탄소성 재료에서는 소성 응력이 항복강도로 항상 일정하다.

$-\frac{h}{2} \leq y \leq -y_e$

$\sigma_x = \sigma_Y$

압축 상태의 소성 영역은 도심에서 $y_e$ 떨어진 영역부터 상단 표면까지가 된다.

$y_e \leq y \leq \frac{h}{2}$

$\sigma_x = -\sigma_Y$

3.4. 굽힘 모멘트와 응력 사이의 관계

미소 모멘트는 미소 영역에 작용하는 힘과 모멘트 거리(arm)의 곱이므로 응력과 도심 거리의 곱이 된다.

$dM = \sigma_x(-y)dA$

굽힘 모멘트는 단면에 작용하는 미소 모멘트를 적분하여 얻는다.

$\begin{align} M &= \int dM \\\\ &= \int_A \sigma_x(-y)dA \end{align}$

다시 응력 구간을 탄성 영역 $A_e$ 와 소성 영역 $A_p$ 로 나누어 적분한다.

$\begin{align} M &= \int_A \sigma_x(-y)dA \\\\ &= \int_{A_e} \sigma_x(-y)dA + \int_{A_p} \sigma_x(-y)dA \end{align}$

위에서 구한 영역별 응력을 이용하면 사각형 단면에 대해 다음과 같이 쓸 수 있다.

$\begin{align} M &= \int_{-y_e}^{y_e} \sigma_x(-y)bdy + \int_{-h/2}^{-y_e}\sigma_Y(-y)bdy + \int_{y_e}^{h/2} -\sigma_Y(-y)bdy \\\\ &= \int_{-y_e}^{y_e} (-\frac{y}{y_e}\sigma_Y)(-y)dy + 2\int_{y_e}^{h/2} (-\sigma_Y)(-y)bdy \end{align}$

정리하면 다음과 같다.

$\begin{align} M &= \frac{b}{y_e}\sigma_Y\int_{-y_e}^{y_e} y^2 dy + 2b\sigma_Y\int_{y_e}^{h/2} y dy \\\\ &= \frac{2}{3}by_e^2\sigma_Y + b\sigma_Y\left(\frac{h^2}{4}-y_e^2\right) \\\\ &= \frac{bh^2}{4}\sigma_Y + \frac{b}{3}y_e^2\sigma_Y \end{align}$

$\therefore M = \frac{bh^4}{4}\sigma_Y\left[1-\frac{4}{3}\left(\frac{y_e^2}{h}\right)\right]$

3.4.1. 소성 임박 상태

위 식에서 $y_e$ 는 탄성과 소성의 경계이다. $y_e$ 가 표면에 있다면 아직 전 영역은 탄성 상태이긴 하나 조금만 하중이 증가하면 소성 변형이 시작되는 소성 임박 상태(impending yielding state)가 된다. 이때 소성 변형이 시작되지는 않았으나 표면의 응력은 항복 응력에 도달한 상태이다.

이 경우의 굽힘 모멘트는 다음과 같다.

$y_e = \frac{h}{2}$

$\begin{align} M &= \frac{bh^2}{4}\sigma_Y\left[1-\frac{1}{3}\right] \\\\ &= \frac{bh^2}{6}\sigma_Y \end{align}$

위에서 구한 소성 임박 상태의 모멘트는 탄성 한계 모멘트(elastic limit moment)이며 항복 모멘트(yielding moment)라고 한다.

$M_Y = \frac{bh^2}{6}\sigma_Y = Z\sigma_Y$

여기에서 $Z$ 는 탄성 단면 모듈러스(elastic section modulus) 또는 줄여서 단면 모듈러스라고 한다. 단면의 형상이 탄성 한계를 결정하는 것이므로 소성이 언제 일어날지 형상 정보만으로 알 수 있게 된다.

$Z = \frac{M_Y}{\sigma_Y} = \frac{bh^2}{6}$

단면 모듈러스는 다시 단면 2차 모멘트로 나타내면 다음과 같다. 여기에서 $c$ 는 두께의 절반으로 중립축에서 표면까지 거리가 된다.

$Z = \frac{I}{c}$

$c = \frac{h}{2}$

3.4.2. 완전 소성 상태

완전 소성 상태(fully plastic state)는 모든 단면이 소성 상태가 된 경우를 말하며 탄성 영역이 존재하지 않으므로 $y_e = 0$ 이다.

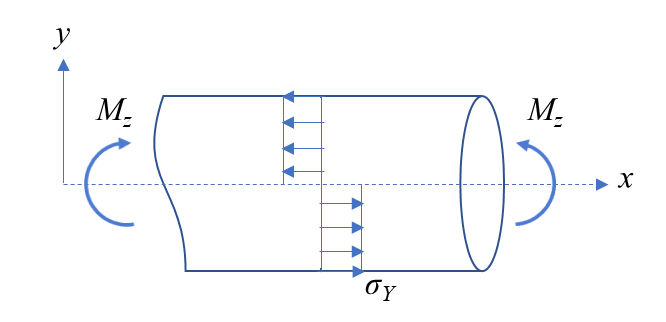
원래 식에 $y_e=0$ 을 대입하여 이 상태의 굽힘 모멘트를 구하면 다음과 같고 이때의 모멘트가 보가 버틸 수 있는 최대 모멘트가 된다. 따라서 소성 모멘트(plastic momont), 한계 모멘트(limit moment), 또는 극한 모멘트(ultimate moment)라고 한다.

$M_P = \frac{bh^2}{4}\sigma_Y = Z_P\sigma_Y$

위 식에서 $Z_P$ 는 소성 단면 계수(plastic section modulus)라고 한다.

$Z_P = \frac{M_P}{\sigma_Y} = \frac{bh^2}{4}$

3.4.3. 형상 계수

지금까지 소성 임박 상태와 완전 소성 상태가 되는 외력 모멘트를 알기 위해 단면의 형상 정보만을 이용하면 된다는 것을 알았다. 이것이 탄성 단면 계수 $Z$ 와 소성 단면 계수 $Z_P$ 이다. 이 두 계수의 비를 형상 계수(Form factor or shape factor)라고 하며 소성이 발생하고 나서 얼마나 더 버틸 수 있는지 알려주는 값이 된다.

$\begin{align} f &= \frac{M_P}{M_Y} \\\\ &= \frac{Z_P\sigma_Y}{Z\sigma_Y} \\\\ &= \frac{Z_P}{Z} \end{align}$

위에서 사각형 단면에 대해 이미 계수들을 구했고 형상 계수를 계산하면 다음과 같다.

$f = \frac{Z_P}{Z} = \frac{bh^2/4}{bh^2/6} = \frac{3}{2}$

원형 단면에 대해서도 구해보자.

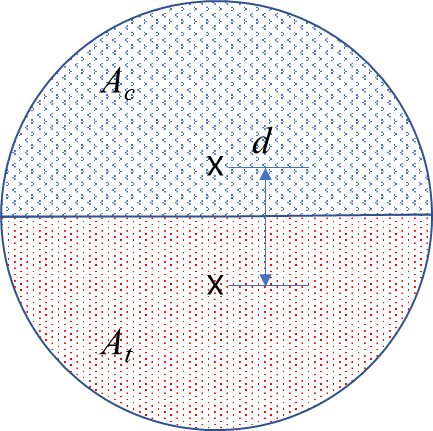
먼저 단면 모듈러스는 다음과 같다.

$Z = \frac{I}{c} = \frac{\frac{\pi}{4} c^4}{c} = \frac{\pi}{4}c^3$

소성 모멘트는 소성 상태에서 작용하는 압축과 인장 응력이 만드는 모멘트이다. 이 응력을 집중 하중으로 생각하면 단면의 도심에 작용하는 경우와 같다. 따라서 압축 단면과 인장 단면의 도심 사이 거리 $d$ 를 이용해 다음과 같이 모멘트를 나타낼 수 있다. 이렇게 작용선이 일치하지 않고 같은 크기의 하중이 반대 방향으로 작용하는 것을 우력(couple)이라고 한다.

$M_P = F_c d = F_t d$

그리고 단면에 작용하는 하중 $F$ 는 다음과 같다.

$\begin{align} F_c &= A_c\sigma_Y = A_t\sigma_Y \\\\ &= \frac{\pi}{2}c^2 \end{align}$

반원의 도심 사이 거리는 반원 도심 거리의 두 배가 되므로 다음과 같다. 심심할 때 직접 구해보자.

$d = \frac{4c}{3\pi} \cdot 2 = \frac{8c}{3\pi}$

따라서 소성 모멘트는 다음과 같다.

$\begin{align} M_P = F_c d &= \frac{\pi}{2}c^2\sigma_Y \cdot \frac{8c}{3\pi} \\\\ &= \frac{4}{3}c^3\sigma_Y \end{align}$

위에서 구한 소성 모멘트를 이용하여 소성 단면 모듈러스를 구하면 다음과 같다.

$Z_P = \frac{M_P}{\sigma_Y} = \frac{4}{3}c^3$

원형 단면의 형상 계수는 다음과 같다.

$\begin{align} f &= \frac{M_P}{M_Y} \\\\ &= \frac{Z_P}{Z} \\\\ &= \frac{\frac{4}{3}c^3}{\frac{\pi}{4}c^3} \\\\ &= \frac{16}{3\pi} \end{align}$

$\therefore f = \frac{16}{3\pi}$

4. 잔류 응력

이전 글에서 단축 인장 상태의 잔류 응력과 비틀림에서의 잔류 응력을 다뤘다. 굽힘도 마찬가지로 소성이 발생한 뒤에 하중을 제거하면 잔류 변형이 남게 된다. 아래 영구 변형률의 아랫첨자는 pastic 또는 permanent, 그리고 residual을 의미한다.

$\varepsilon_p = \varepsilon_r$

잔류 문제는 늘 그렇듯이 하중이 인가된 상태에 반대 방향으로 하중을 작용하여 중첩(superposition)하는 방법으로 구한다. 따라서 제하 과정은 역 방향의 외력이 작용하는 것이며 탄성 거동을 한다. 또 탄성 거동을 하므로 Hooke's law가 성립한다.

위 그림 1의 경우에서 변형률은 다음과 같다.

$\varepsilon_x = -\frac{y}{\rho} = -\frac{y}{y_e}\varepsilon_Y$

각 부분의 응력은 다음과 같다.

(1) $-y_e < u < y_e$ : elastic region

$\sigma_x = E\varepsilon_x = -\frac{y}{y_e}\sigma_Y$

(2) $-h/2 \leq y \leq -y_e$

$\sigma_x = \sigma_Y$

(3) $y_e \leq y \leq h/2$

$\sigma_x = -\sigma_Y$

4.1. 굽힘 모멘트

작용한 굽힙 모멘트를 다시 한번 쓰면 아래와 같다.

$M = \frac{bh^4}{4}\sigma_Y\left[1-\frac{4}{3}\left(\frac{y_e^2}{h}\right)\right]$

4.2. 잔류 응력

잔류 응력은 다음과 같이 구한다.

$\sigma_r = \sigma_x + \sigma_u$

여기에서 $\sigma_x$ 하중이 가해졌을 때 발생하는 응력, $\sigma_u$ 는 제하 응력이다. $\sigma_u$ 는 굽힙 응력 식에 외력과 크기가 같고 방향이 반대인 가상의 굽힘 모멘트를 적용한 것이다.

$\sigma_u = -\frac{(-M)}{I}y = \frac{M}{I}y$

4.2. 잔류 변형률

잔류 변형률은 인가 변형률과 제하 변형률의 중첩으로 구한다.

$\varepsilon_r = \varepsilon_x + \varepsilon_u$

여기에서 $\varepsilon_x$ 는 하중이 가해졌을 때 발생하는 변형률, 역방향 하중에 의하 발생하는 $\varepsilon_u$ 는 제하 변형률이다.

$\begin{align} \epsilon_u &= \frac{\sigma_u}{E} = \frac{My}{EI} \\\\ \varepsilon_x &= \frac{y}{y_e}\varepsilon_Y = -\frac{y}{y_e}\frac{\sigma_Y}{E} \end{align}$

4.3. 잔류 곡률

소성이 시작된 위치 $y_e$ 에서의 변형률은 다음과 같다.

$\varepsilon_Y = \varepsilon_x|_{y=-y_e} = \frac{y_e}{\rho}$

$\therefore \kappa = \frac{1}{\rho} = \frac{\varepsilon_Y}{y_e} = \frac{\sigma_Y}{Ey_e}$

잔류 곡률(residual curvature)도 중첩을 이용해 구한다.

$\kappa_r = \kappa + \kappa_u$

또는 다음과 같이 곡률 반경으로 표현할 수도 있다.

$\frac{1}{\rho_r} = \frac{1}{\rho} + \frac{1}{\rho_u}$

여기에서 각 항은 다음과 같다.

$\begin{align} \frac{1}{\rho} &= \frac{\sigma_Y}{Ey_e} \\\\ \frac{1}{\rho_u} &= -\frac{M}{EI} \\\\ \varepsilon_u &= -\frac{y}{\rho_u} = \frac{\sigma_u}{E} = \frac{M}{EI}y \end{align}$

저작자표시 비영리

내 블로그 - 관리자 홈 전환	`Q` `Q`
새 글 쓰기	`W` `W`

글 수정 (권한 있는 경우)	`E` `E`
댓글 영역으로 이동	`C` `C`

이 페이지의 URL 복사	`S` `S`
맨 위로 이동	`T` `T`
티스토리 홈 이동	`H` `H`
단축키 안내	`Shift` + `/` `⇧` + `/`

소성 굽힘 (Plastic Bending)

1. 소성이 발생한 보

2. 재료와 경도