1. 전단 중심 (Shear Center)
1.1. 전단 중심
전단 중심이란 단면에 비틀림이 발생하지 않도록 전단력이 작용해야할 위치를 말한다.
∑Mx=0
대칭 중실 단면(solid section)은 도심이 전단 중심이다. 도심을 향해 하중을 작용하면 굽힘만 발생할 것이다.
폐단면의 경우에도 대칭인 경우에는 도심이 전단 중심이 된다.
위 두 경우에서 하중이 단면의 도심을 향해 작용한다면 부재는 비틀림 없이 굽힘만 발생하게 된다. 그러나 대칭이 아닌 단면의 경우에는 도심을 향해 하중이 작용할 경우 부재가 비틀어지게 된다. 비대칭 개단면의 전단 중심은 그림 3과 같다. 대칭인 축은 도심과 일치하지만 비대칭인 축은 전단 중심의 위치가 도심과 다르다.
이런 경우 구조물에 굽힘과 비틀림이 동시에 발생하게 되면 다음과 같은 전단 응력을 받는다.
τ=τd+τt=VQIt+TIpr
위 식에서 τd는 direct shear stress로 굽힘에 의해 직접 발생하는 전단 응력이며 τt는 비틀림에 의해 부차적으로 발생하는 전단 응력이다. 우리가 구조 설계를 할 때 구조물의 거동을 보다 단순화 하고 더 큰 하중을 버티게 하려면 비틀림 없이 굽힘만 발생하도록 설계하는 것이 당연히 좋을 것이다. 특히 개단면은 폐단면에 비해 비틀림에 매우 취약하다. 따라서 부재의 하중점이 전단 중심이 되도록 해야하며 부재의 연결부는 전단중심이 되어야 한다.
2. 전단 중심의 예
아래 예제에서 나타낸 모든 단면은 하중이 작용하는 면이 아닌 그 반대쪽 단면이다. 만약 하중이 작용하는 단면을 선택한다면 그 단면에서는 내력과 외력의 평형 방정식이 성립하지 않는다. 자유 물체도를 그리고 확인해보자.
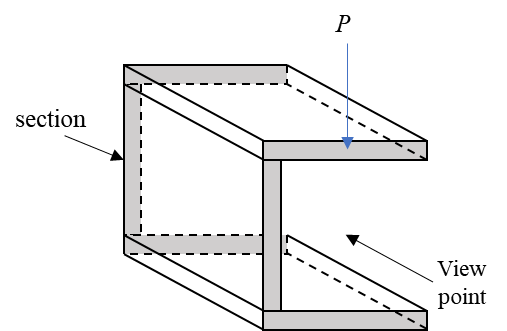
하중이 작용하는 단면의 내력은 남겨진 물체의 단면이 하중면이 되도록 길이 방향을 극한으로 보내 얻을 수 있다. 이 경우 내력의 방향은 하중의 방향과 일치하게 된다는 것을 알 수 있다. 다시 말해 이 경우는 내력은 곧 외력의 성분 분할이며 견인력(traction)이라고도 한다.
2.1. 앵글 (angle)
다음 그림 5과 같은 앵글 부재에 하중이 작용해야 한다고 하자. 교차점 O로 부터 얼마나 떨어진 거리에 하중이 작용해야 비틀림이 없는지 구해보자.
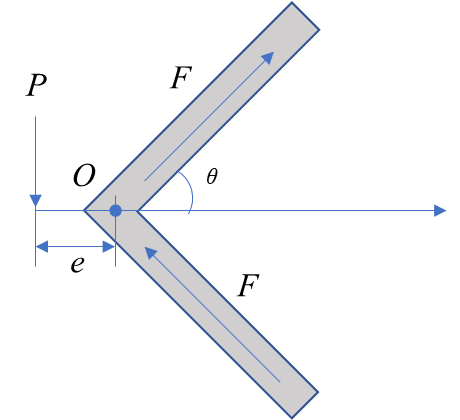
먼저 O점에 대해 모멘트에 대한 평형 방정식을 세우면 아래와 같다.
∑M=Pe−F(0)−F(0)=0
∴
앵글의 전단 중심은 교차점에 있다는 것을 알 수 있다.
내력 F는 하중 평형을 이용해 다음과 같이 구할 수 있다.
\sum{F_y} = -P + F\sin\theta + F\sin\theta = 0
\therefore F = \frac{P}{2\sin\theta}
전단 흐름을 이용해 구해도 같은 결과를 얻을 수 있다.
위 그림 6에서 빗금친 영역에 전단 흐름 q가 흐른다고 보면 끝단에서의 거리 s에 대해 전단 흐름을 적분하여 전단력을 구할 수 있다.
F = \int_0^a qds = \int_0^a \frac{VQ}{I}ds
여기에서 빗금친 영역의 도심 거리 \bar{y_0}와 면적 A_0는 다음과 같다.
\begin{align} \bar{y_0} &= \left(a-\frac{1}{2}s\right)\sin\theta \\\\ A_0 &= st \end{align}
따라서 Q는 다음과 같다.
Q = A_0\bar{y_0} = st\left(a-\frac{1}{2}s\right)\sin\theta
전단력 V는 하중 P와 평형을 이루고 있고 전단 흐름을 적분하면,
\begin{align} V &= \int_0^a qds = \int_0^a \frac{VQ}{I}ds \\\\ &= \int_0^a \frac{P}{I}st\sin\theta ds \\\\ &= \frac{Pt}{I}\sin\theta \int_0^a \left(as - \frac{1}{2}s^2\right) ds \\\\ &= \frac{Pt}{I}\sin\theta \left[\frac{1}{2}as^2 - \frac{1}{6}s^3\right]_0^a \\\\ &= \frac{Pt}{3I}a^3\sin\theta \end{align}
\therefore F = \frac{Pt}{3I}a^3\sin\theta
I는 그림 7처럼 단면에 대한 2차 모멘트를 적분하여 다음과 같이 구할 수 있다.
\begin{align} I &= \int_0^a y^2 dA \\\\ &= 2\int_0^a (s\sin\theta)^2 (tds) \\\\ &= 2t\sin^2\theta \int_0^a s^2 ds \\\\ &= \frac{2}{3}ta^3\sin^2\theta \end{align}
\therefore I = \frac{2ta^3}{3}\sin^2\theta
마지막으로 위에서 구한 F 식에 I를 대입하여 계산하면,
\begin{align} F &= \frac{Pt}{3I}a^3\sin\theta \\\\ &= \frac{Pt}{3}a^3\sin\theta \times \frac{3}{2ta^3}\frac{1}{\sin^2\theta} \\\\ & = \frac{P}{2\sin\theta} \end{align}
\therefore F = \frac{P}{2\sin\theta}
두 결과가 동일함을 알 수 있다.
2.2. 채널 (channel)
전단 중심의 예로 가장 많이 쓰이는 ㄷ자형 채널 단면의 경우를 살펴보자.
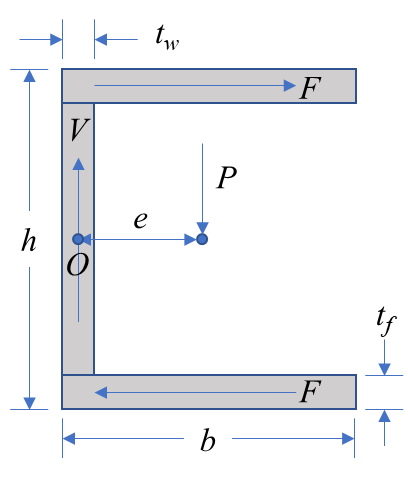
위 채널 단면에서 평형 방정식을 이용해 내력과 전단 중심을 구해보자
\sum F_y = P - V = 0
\therefore V = P
\sum F_x = F - F = 0
\sum M_x|_O = -Pe - Fb = 0
\therefore e = -\frac{F}{P}h
전단 중심의 위치는 e = -(F/P)h에 있다. 다시 말해 도심도 아니고 채널 단면의 바깥에 존재하는 것이다. 다시 그림 12를 보면 전단 중심의 위치 e가 O점의 왼쪽에 있을 때 F가 만드는 모멘트가 시계 방향이고 P가 만드는 모멘트가 반시계 방향으로 서로 상쇄된다는 것을 알 수 있다. V는 모멘트 팔이 없기 때문에 V가 만드는 모멘트는 없다. 따라서 이런 채널 단면의 보가 굽힘 하중을 받을 때는 다음과 같이 접속부를 설계하여 하중점이 외부에 있도록 할 필요가 있다.
이제 전단 중심이 바깥에 있다는 것은 파악했으니 구체적인 위치를 계산해 볼 차례다. 위에서 구한 전단 중심의 위치에서 모르는 값은 내력 F이다. F는 다음과 같이 구할 수 있다.
먼저 플랜지에 작용하는 내력 F는 전단 흐름을 적분하여 구할 수 있다.
F = \int_0^b \tau_{xz} t_f ds
플랜지에 작용하는 전단 응력은 다음과 같다.
\tau_{xz} = \frac{VQ_s}{I_z t_f}
그림 13에서 빗금친 영역의 면적을 A_0라고 하고 도심 거리를 \bar{y_0}라고 하자.
A_0 = t_fs
\bar{y_0} = \frac{h}{2}
따라서 Q_s는 다음과 같다.
Q_s = A_0\bar{y_0} = \frac{hst_f}{2}
다시 전단 응력을 구하면 다음과 같다.
\tau_{xz} = \frac{P(hst_f/2)}{I_z t_f} = \frac{Psh}{2I_z}
다시 내력 F를 구하면 다음과 같다.
\begin{align} F &= \int_0^b \frac{Psh}{2I_z} t_f ds \\\\ &= \frac{Pht_f}{2I_z} \int_0^b s ds \\\\ & = \frac{Ph}{4I_z}t_fb^2 \end{align}
다시 기하 형상에 대한 전단 중심의 위치를 구하면 다음과 같다.
\therefore e = -\frac{h^2t_fb^2}{4I_z}
단면의 2차 모멘트 I_z는 평행축 정리를 이용해 다음과 같이 구한다.
\begin{align} I_z &= \frac{t_w h^3}{12} + 2\left[\frac{b t_f^3}{12} + bt_f\left(\frac{h}{2}\right)^2\right] \\\\ &= \frac{t_w h^3}{12} + \frac{bt_fh^2}{2} \end{align}
위 식의 두번째 줄에서 얇은 단면에 대해 t_f^3 \approx 0이므로 무시했다.
최종적으로 전단 중심의 위치는 다음과 같다.
\therefore e = -\frac{h^2b^2t_f}{6bt_f + ht_w}
최근댓글