1. 두께가 얇은 단면 (Thin-walled Section)
어떤 가늘고 긴 부재가 비틀림이나 굽힘을 받을 때 무게 대비 효율을 최대하는 방법은 속을 비우는 것이다. 비틀림에서는 도심에서 멀수록 큰 토크를 감당하고 도심 부근에서는 토크를 거의 부담하지 않기 때문에 파내도 된다.
$$ \tau = \frac{T}{I_p}r $$
굽힘에서는 재료가 도심에서 멀리 퍼져있을 수록 단면 2차 모멘트가 커져 굽힘 강성이 증가하므로 유리하다. 따라서 굽힘 강성에 영향이 미미한 내부를 파내는 것이 좋다. 무게가 줄면 자중에 의한 처짐도 줄고 운송도 쉬워진다. 이런 장점이 내부를 파내서 발생하는 강성의 손실보다 크다고 할 수 있다.
$$ \sigma = -\frac{M}{I}y $$
이런 이유로 구조물을 설계할 때 단면의 외각 치수는 크지만 두께는 얇은 부재를 이용하게 된다. 중공 원형 단면을 갖는 파이프나 형강이 이에 해당한다. 이런 얇은 두께를 갖는 단면을 thin-walled section이라 한다. 그리고 관(pipe)와 같이 틈(gap or crack)이 없는 형태를 닫힌 단면 또는 폐단면(closed section)이라 하고 형강과 같은 것은 열린 단면 또는 개단면(opened section)이라 한다. 균열이 있는 관이나 두께가 얇은 형강은 thin-walled open section이 된다.

2. 전단 흐름 (Torsional Shear Flow)
위 비틀림 전단 응력 식을 보면 전단 응력은 중심에서 떨어진 거리에 따라 달라진다. 이때 단면의 두께 $t$가 아주 얇다면 두께방향으로의 전단 응력 차이는 거의 무시할 수있을 것이다. 따라서 두께가 얇은 부재에서 전단 응력은 두께 $t$에 작용하는 평균 전단 응력으로 생각하는 것이 편리하다. 이제 다음 그림 2와 같이 얇은 단면의 한 조각에서 평형을 생각해보자.
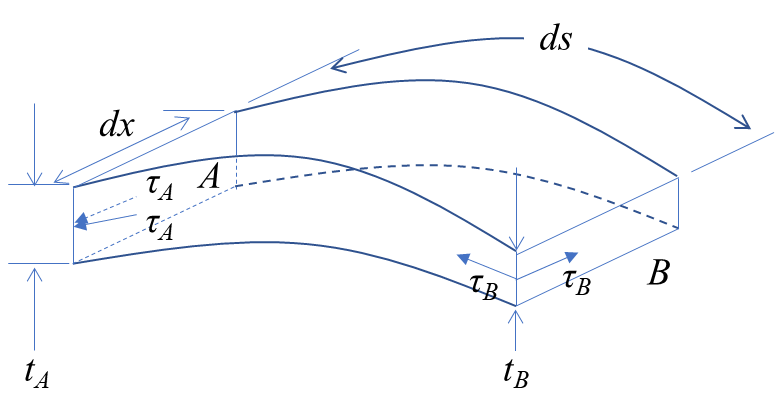
그림 2에서 A면과 B면의 두께는 $t_A$와 $t_B$로 다르다. 그리고 두 면은 도심에서의 거리도 달라 전단 응력도 같지 않다고 하자. 일단 $x$방향 단면에서의 전단 응력은 부재에 작용하는 토크와 같은 방향으로 작용할 것이다.
이제 위 조각에 대해 평형 방정식을 세워보자. A면에 작용하는 힘과 B면에 작용하는 전단력은 서로 평형을 이뤄야하므로 크기가 같고 방향은 반대일 것이다.
$$ \sum V = \tau_A t_A dx - \tau_B t_B dx = 0 $$
위 식에서 $dx$를 소거하면 다음과 같은 식을 얻는다.
$$ \tau_A t_A = \tau_B t_B $$
위 식은 어떤 위치에서 전단응력과 두께의 곱은 항상 일정하다는 것을 의미한다. 전단 흐름 $q$를 일정한 유량(flow)라고 생각하면 폭 $t$가 좁을 경우 전단 응력 $\tau$가 커지고 폭이 넓은 경우 전단 응력이 작아진다. 이제 우리는 이 전단 응력과 두께의 곱을 전단 흐름(shear flow)이라고 정의하고 아래와 같이 쓴다.
$$ q = \tau t = \text{constant} $$
위 조각에 작용하는 전단력이 $V = \tau t ds$가 되므로 전단 흐름은 $q = \tau t = V/ds$가 된다. 따라서 전단 흐름의 단위는 단위 길이당 전단 하중이다.
$$ q = \tau t = \frac{V}{ds} $$
2.1. 비틀림 (Torsion)
2.1.1. 비틀림 전단 흐름
비틀림 상태에서 전단 흐름은 그림 3처럼 나타낼 수 있다.

이때 토크와 전단 흐름의 관계는 다음과 같다.
\begin{align} dT &= q \cdot ds \cdot r \\\\ &= qr \cdot ds \end{align}

$dT$를 폐단면에서 적분하면,
\begin{align} T &= \oint dT \\\\ &= \oint qr \cdot ds \\\\ &= q \oint rds \\\\ &= q(2A_m) \end{align}
$$ \therefore q = \frac{T}{2A_m} $$
여기에서 $A_m$은 sectional area라고 하며 두께의 반으로 구성된 폐단면적으로 다음과 같다. $r$과 $ds$가 이루는 삼각형 면적을 한바퀴 돌면서 합친 면적이라고 생각하면 된다.
$$ A_m = \frac{1}{2}\oint r ds $$
2.1.2. 비틀림 전단 응력
전단 응력은 다음과 같이 구할 수 있다.
$$ \tau = \frac{q}{t} = \frac{T}{2qA_mt} $$
$$ \therefore \tau = \frac{T}{2qA_mt} $$
여기에서 sectional area $A_m$은 다음과 같다.
\begin{align} A_m &= \frac{1}{2}\oint rds \\\\ &\approx \frac{1}{2}(A_i + A_o) \end{align}
$A_i$는 내부 경계에 의한 면적(inner perimetric area)이고 $A_o$는 외부 경계에 의한 면적(outter perimetric area)를 말한다. $A_m, A_i$ 그리고 $A_o$를 그림 3에 나타냈다.

2.1.3. 비틀림 변형률 에너지
비틀림 변형률 에너지(torsional strain energy)는 다음과 같다.
$$ U = \int_V u_0 dV $$
$u_0$는 변형률 에너지 밀도(strain energy density)이다.
\begin{align} u_0 &= \int_V \frac{1}{2}\tau \gamma dV \\\\ &= \frac{1}{2}\frac{\tau^2}{G} = \frac{1}{2G}\left[ \frac{T}{2A_mt}\right]^2 \\\\ &= \frac{T^2}{8GA_m^2t^2} \end{align}
따라서 비틀림 변형률 에너지는 다시 다음과 같이 구할 수 있다.
\begin{align} U &= \frac{T^2}{8GA_m^2t^2} \\\\ &= \int_0^L \frac{T^2}{8GA_m^2}\left[\int_A \frac{dA}{t^2}\right] dx \end{align}
여기에서 $dA = tdS$이므로,
$$ \int_A \frac{dA}{t^2} = \oint\frac{t}{t^2}ds = \oint\frac{ds}{t} $$
$$ \therefore U = \int_0^L \frac{T^2}{8GA_m^2}\left[\oint\frac{ds}{t}\right]dx $$
흔히 사용하는 축부재는 $G, A_m, T$가 일정한 prismatic bar이며 이 경우에는 다음과 같이 정리할 수 있다.
$$ U = \frac{T^2L}{8GA_m^2}\oint\frac{ds}{t} $$
2.1.4. 비틀림 각
외부에서 토크가 축에 한 일(external work)은 다음과 같다. $K_t$는 비틀림 강성이다.
\begin{align} W &= \int_0^\Delta Pd\Delta \\\\ &= \int_0^\Phi Td\Phi \\\\ &= \int_0^\Phi K_t\Phi d\Phi \\\\ &= K_t \cdot \frac{\Phi^2}{2} \\\\ &= \frac{1}{2}(K_t\cdot \Phi) \Phi \\\\ &= \frac{1}{2}T\Phi \end{align}
$$ \therefore W = \frac{1}{2}T\Phi $$
에너지 보존 법칙에 의해 외력이 한 일은 변형률 에너지와 같다.
$$ U = W $$
따라서 prismatic bar에 대해 다음과 같이 쓸 수 있다.
$$ \frac{T^2L}{8GA_m^2}\oint\frac{ds}{t} = \frac{1}{2}T\Phi $$
따라서 비틀림 각은 다음과 같이 구할 수 있다.
$$ \Phi = \frac{TL}{4GA_m^2}\oint\frac{ds}{t} $$
지금까지 위에서 구한 폐단면의 여러가지 식을 이전에 얻은 비틀림의 식과 비교해볼 수 있다. 단순한 대칭 형태의 중공 단면을 이용해 확인해보면 두 결과가 동일하다는 것을 확인할 수 있다. 그러나 단면의 형상이 복잡하다면 위의 폐단면 식을 이용해 구조물의 거동을 예측할 수 있다.
2.2 굽힘 (Bending)
앞서 보의 굽힘에서 발생하는 전단 응력을 다음과 같이 구했다.
$$ \tau = \frac{VQ}{Ib} $$
여기에서 단면의 폭 $b$가 아주 작아서 얇게 된다고 하자. 구분을 위해 얇은 두께를 $t$라고 다시 쓴다.
$$ b \rightarrow t $$
전단 응력은 다시 얇은 두께 $t$에 대해 다음과 같이 쓸 수 있다.
$$ \tau = \frac{VQ}{It} $$
$$ \text{where, } Q = \int_{A_0}ydA = A_0\bar{y_0} $$
비틀림에서와 달리 굽힘에서는 전단흐름 $q$가 일정하지 않다. 지난 글에서 우리는 굽힘의 경우 도심에서 전단 응력이 최대가 되고 바깥면에서는 작용하지 않는 것을 확인했다. 따라서 굽힘에서의 전단 흐름은 다음과 같다.
$$ q = \tau t = \frac{VQ}{I} $$
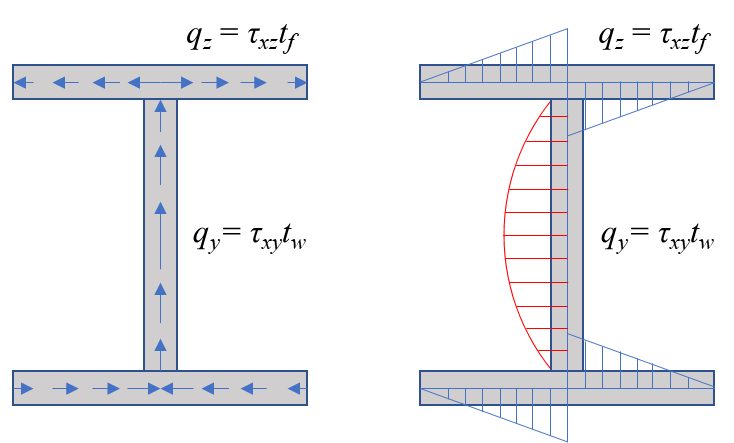
그림 4를 보면 전단 흐름은 일정하지 않다. 굽힘에 대한 전단 응력은 포물선으로 분포하므로 웨브(web)에서 전단흐름 역시 도심에서 최대가 되고 끝단에서 0이 된다. 플랜지(flange)에서는 선형으로 분포한다. 주의할 점은 어떤 저자는 모두 같은 $q$로 표기하는 경우가 많지만 flange와 web에서의 전단 흐름은 그 응력 성분의 출처가 다르다는 것을 알고 있어야 한다. 위 그림 4에는 좌표계를 표시하지 않았지만 보의 길이 방향(지면을 뚫고 나오는 방향)이 $x$축이고 세로 방향이 y축이다.
이제 공부를 열심히 한 사람은 의문을 가지게 된다. 플랜지에 작용하는 굽힘에 의한 전단 응력도 $\tau_{xy}$만 있을 것 같은데 왜 $\tau_{xz}$가 나오느냐 하는 것이다. 물론 $\tau_{xy}$도 존재하고 계산에 반영하겠지만 이 $\tau_{xz}$가 어째서 존재하는지에 대한 의문을 풀어야 한다.
플랜지의 끝단을 절단하여 자유물체도를 그리면 그림 5와 같다. 절단부의 $x$방향 단면적을 $A_0$라고 하자.

이 자유 물체도에 대한 평형을 고려하면 다음과 같다.
$$ \sum F_x = \int_{A_0} \sigma|_{x+\Delta x} dA - \int_{A_0} \sigma|_x dA - F = 0 $$
굽힘 응력은 다음과 같다.
$$ \sigma = -\frac{M_by}{I_z} $$
내력 $F$를 굽힘 응력에 대해 정리하면 다음과 같다.
\begin{align} F &= -\int_{A_0} \frac{M_b|_{x+\Delta x}y}{I_z} dA + \int_{A_0} \frac{M_b|_{x}y}{I_z} \\\\ &= -\frac{M_b|_{x+\Delta x} - M_b|_{x}}{I_z} \int_{A_0} y dA \end{align}
여기에서 $x+\Delta x$ 위치에서 모멘트에 대한 테일러 급수 전개를 하고 1차 항까지만 고려하면 다음과 같다.
$$ M_b(x + \Delta x) = M_b(x) + \frac{dM_b(x)}{dx}\Delta x $$
$$ \frac{M_b|_{x+\Delta x} - M_b|_{x}}{I_z} = \frac{dM_b(x)}{dx}\Delta x $$
다시 굽힙 모멘트의 미분은 전단력과 같다.
$$ \frac{dM_b}{dx} = -V $$
따라서 내력 $F$는 다음과 같이 표현할 수 있다.
$$ F = \frac{V}{I_z}\Delta x \int_{A_0} y dA $$
양변을 $\Delta x$로 나누면 좌변은 단위 길이당 내력이므로 전단 흐름이 된다.
$$ \frac{F}{\Delta x} = q_z = \tau_{zx} t_f = \tau_{xz} t_f $$
따라서 플랜지에 작용하는 전단 응력은 다음과 같다.
$$ \tau_{xz} = \frac{VQ_s}{I_z t_f} $$
$Q_s$는 플랜지의 개방단에 $s$만큼 떨어진 거리까지에 해당하는 면적의 도심에 대한 단면 2차 모멘트이다.
$$ Q_s = \int_{A_0} y dA $$




최근댓글