1. 분포 하중과 전단 응력, 그리고 모멘트
1.1. 분포 하중이 작용하는 보
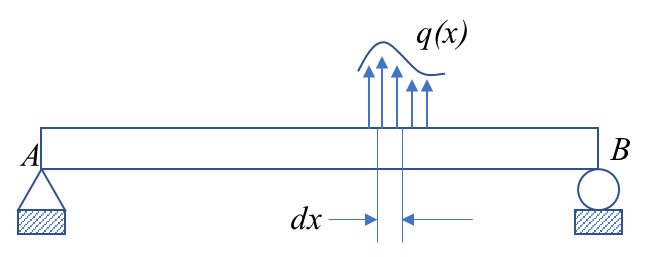
그림 1과 같은 보에 $q(x)$의 분포 하중(distributed load)가 작용하고 있다. 여기에서 아주 작은 크기 $dx$에 해당하는 부분을 확대해서 그림 2에 나타내고 하중 상태를 표시했다. 특별한 것은 없고 구배(gradient)에 의한 하중 증분이 반영되어 있다.
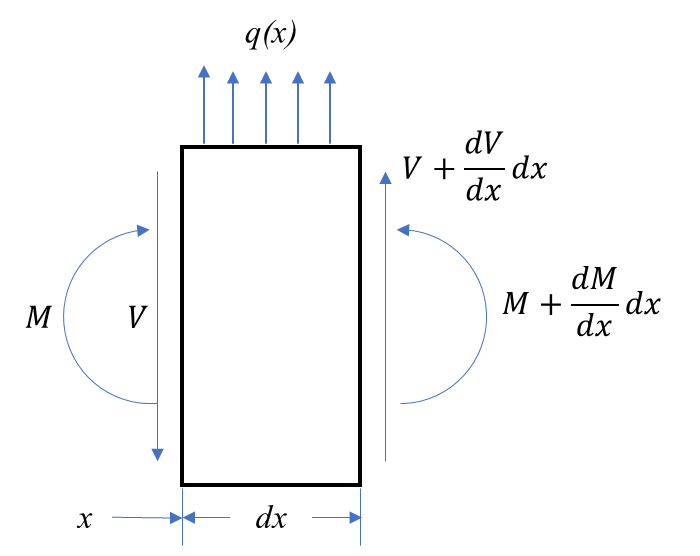
1.2. 힘의 평형(Force Equilibrium)
그림 2에서 힘의 평형 방정식은 다음과 같다.
$$ \sum{F_y} = -V + \left(V + \frac{dV}{dx}dx\right) + q(x)dx = 0 $$
$$ \therefore \frac{dV}{dx} + q(x) = 0 $$
1.3. 모멘트의 평형(Moment Equilibrium)
모멘트 평형은 다음과 같다.
$$ \sum{M_z}|_{x+dx} = -M + \left(M + \frac{dM}{dx}dx\right) + Vdx - q(x)dx\left(\frac{dx}{2}\right) = 0 $$
위 식에서 마지막 항의 ${dx}^2$은 아주 작은 $dx$를 제곱한 것으로 나머지 항에 비해 너무너무 작기 때문에 무시할 수 있다.
$$ \therefore \frac{dM}{dx} + V = 0 $$
1.4. 모멘트와 분포 하중 사이의 관계
위의 모멘트 평형의 결과로 모멘트와 전단 응력의 관계를 구했다.
$$ \frac{dM}{dx} = -V(x) $$
위 식을 한 번 더 미분 해보자.
$$ \frac{d^2M}{{dx}^2} = -\frac{dV}{dx} $$
힘의 평형에서 전단 응력의 미분은 분포 하중이 됨을 알 수 있었다.
$$ \frac{dV}{dx} = -q(x) $$
따라서 모멘트와 분포 하중은 다음 관계를 갖는다.
$$ \therefore \frac{d^2M}{{dx}^2} = q(x) $$
2. 예제

그림 3에 등분포 하중 $-q_0$가 작용하는 보를 나타냈다.
2.1. 반력의 결정
평형 방정식은 다음과 같다.
\begin{align} \sum{F_x} &= A_x = 0 \\\\ \sum{F_y} &= A_y + B_y - q_0L = 0 \\\\ \sum{M_z}|_A &= B_yL -q_0L\cdot\frac{L}{2} = 0 \end{align}
$$ \therefore A_y = B_y = \frac{q_0L}{2} $$
2.2. 내력의 결정

그림 4와 같이 $x$ 위치에서의 내력을 구해보자. 자동으로 평형 방정식을 만들어야 한다.
\begin{align} \sum{F_x} &= A_x + F = 0 \\\\ \sum{F_y} &= A_y + V - q_0x = 0 \\\\ \sum{M_z}|_A &= = -q_0x\cdot\frac{x}{2} + Vx + M = 0 \end{align}
위 식을 정리해서 내력을 구하면 다음과 같다.
\begin{align} F &= 0 \\\\ V &= q_0x - A_y \\\\ &= q_0x - \frac{q_0L}{2} \\\\ M &= \frac{q_0x^2}{2} - Vx \\\\ &= \frac{q_0x^2}{2} - q_0x^2 - \frac{q_0Lx}{2} \\\\ &= -\frac{q_0x^2}{2} - \frac{q_0Lx}{2} \end{align}
\begin{align} \therefore F &= 0 \\\\ V &= q_0x - \frac{q_0L}{2} \\\\ M &= -\frac{q_0x^2}{2} + \frac{q_0Lx}{2} \end{align}
2.3. 전단 응력과 분포 하중
위에서 구한 전단 응력을 미분해보자.
$$ \frac{dV}{dx} = \frac{d}{dx}\left(q_0x - \frac{q_0L}{2}\right) = q_0 $$
이 예제에서 분포 하중은 다음과 같다.
$$ q(x) = -q_0 $$
따라서 다음 분포 하중과 전단 응력 사이의 관계가 성립한다.
$$ \frac{dV}{dx} = -q(x) = q_0 $$
2.4. 굽힘 모멘트와 전단 응력
위에서 구한 굽힘 모멘트를 미분해보자.
$$ \frac{dM}{dx} = \frac{d}{dx}\left(-\frac{q_0x^2}{2} + \frac{q_0Lx}{2}\right) = -q_0x + \frac{q_0L}{2} $$
위에서 구한 전단 응력은 다음과 같다.
$$ V = q_0x - \frac{q_0L}{2} $$
따라서 굽힘 모멘트와 전단 응력 사이의 관계가 성립한다.
$$ \frac{dM}{dx} = -V(x) = -q_0x + \frac{q_0L}{2} $$
2.5. 굽힘 모멘트와 분포 하중
굽힘 모멘트를 두 번 미분하면 다음과 같다.
$$ \frac{d^2M}{{dx}^2} = \frac{d^2}{{dx}^2}\left(-\frac{q_0x^2}{2} + \frac{q_0Lx}{2}\right) = -q_0 $$
따라서 다음의 관계가 성립한다.
$$ \frac{d^2M}{{dx}^2} = q(x) $$




최근댓글