1. 평행 축 정리 (Parallel Axis Theorem)
평행축 정리는 단면 2차 모멘트를 평행 이동된 다른 좌표계에 대해서 구할 때 유용하다. H beam이나 I beam과 같이 복잡한 단면 형상의 경우 간단한 사각형으로 나누고 평행축 정리를 이용해 결과를 조합하면 쉽게 단면 2차 모멘트를 구할 수 있다.

그림 1과 같이 도심을 원점으로 하는 좌표계 $z-y$가 있다. 이 좌표계를 평행 이동한 $z'-y'$ 좌표계를 생각해보자. 새로운 좌표계에 대한 도심의 위치는 $(\bar{z}, \bar{y})$가 된다. 그림 1에 나타낸 단면의 면적을 $A$라고 하면 아래와 같이 $z'-y'$ 좌표계에서의 단면 1차 모멘트를 생각할 수 있다.
$$ \int_A y dA = A\bar{y} $$
$$ \int_A z dA = A\bar{z} $$
새로운 좌표계에서 $z'$축에 대한 단면 2차 모멘트는 다음과 같다.
\begin{align} I_{z'} &= \int_A y'^2 dA \\\\ &= \int_A (y+\bar{y})^2 dA \\\\ &= \int_A y^2 + 2y\bar{y} + \bar{y}^2 dA \\\\ &= \int_A y^2 dA + 2\bar{y}\int_A y dA + \int_A \bar{y}^2 dA \\\\ &= I_z + 0 + A\bar{y}^2 \end{align}
도심에 대한 단면 1차 모멘트는 0이기 때문에 아래처럼 간단하게 정리할 수 있다.
$$ \therefore I_{z'} = I_z + A\bar{y}^2 $$
마찬가지로 $I_{y'}$에 대해 전개하면 아래와 같다.
\begin{align} I_{y'} &= \int_A z'^2 dA \\\\ &= \int_A (z+\bar{z})^2 dA \\\\ &= I_y + A\bar{z}^2 \end{align}
단면의 상승 모멘트에 대해 전개하면 다음과 같다.
\begin{align} I_{yz} &= \int_A y'z' dA \\\\ &= \int_A (y+\bar{y})(z+\bar{z}) dA \\\\ &= \int_A yz dA + \bar{z}\int_A y dA + \bar{y}\int_A z dA + \bar{y}\bar{z} \int_A dA \\\\ &= I_{yz} + A\bar{y}\bar{z} \end{align}
평행 축 정리 (Parallel Axis Theorem)
\begin{align} I_{y'} &= I_y + A\bar{z}^2 \\\\ I_{z'} &= I_z + A\bar{y}^2 \\\\ I_{y'z'} &= I_{yz} + A\bar{y}\bar{z} \end{align}
또는,
\begin{align} I_{y} &= I_{y'} - A\bar{z}^2 \\\\
I_{'} &= I_{z'} - A\bar{y}^2 \\\\ I_{yz} &= I_{y'z'} - A\bar{y}\bar{z} \end{align}
2. 형강(Shaped Steel)의 단면 2차 모멘트
아래 그림 2와 같이 복잡한 형태를 갖는 형강의 단면 2차 모멘트를 구해보자. 실제 구조재로 자주 쓰이는 형태이다. 우리는 사각형 형상에 대한 단면 2차 모멘트를 이미 알고 있으므로 형강을 사각형 세 개로 쪼개서 생각하면 편리하다.
\begin{align} A &= A_1 + A_2 +A _3 \\\\ A_1 &= b_1t_1 \\\\ A_2 &= b_2t_2 \\\\ A_3 &= b_3t_3 \end{align}
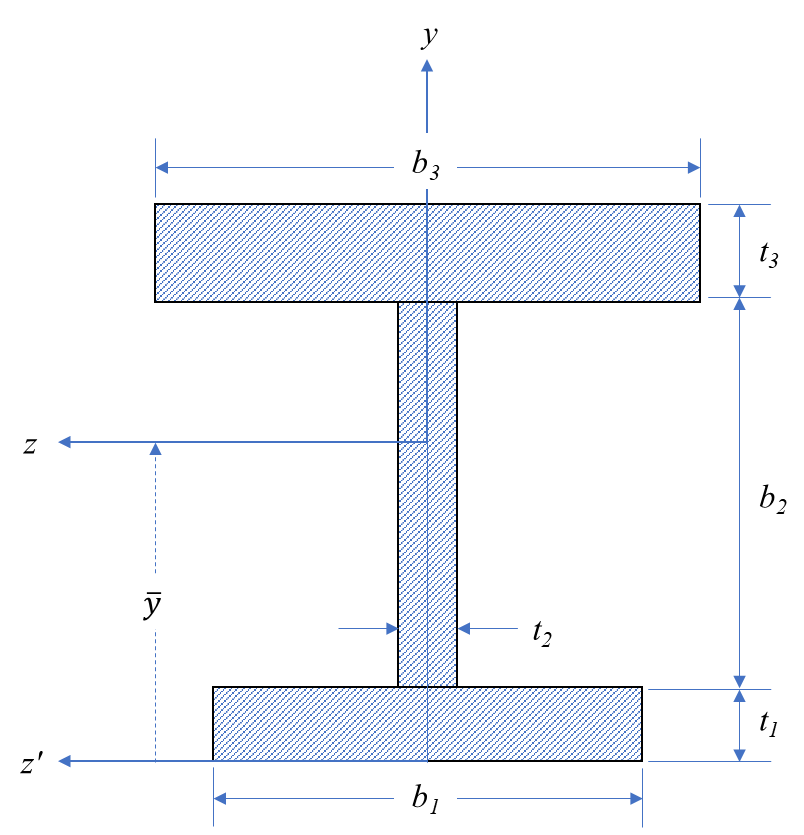
2.1. 도심의 위치
$z'-y$ 좌표계에 서 $y$ 축 방향 도심의 위치는 다음과 같이 구할 수 있다.
$$ \bar{y} = \frac{1}{A}\left(A_1\bar{y_1} + A_2\bar{y_2} + A_3\bar{y_3} \right) $$
각 조각 별 도심의 위치는 다음과 같다.
\begin{align} \bar{y_1} &= \frac{t_1}{2} \\\\ \bar{y_2} &= t_1 + \frac{b_2}{2} \\\\ \bar{y_3} &= t_1 + b_2 + \frac{t_3}{2} \end{align}
2.2. 단면의 2차 모멘트
먼저 각 조각 별 단면의 2차 모멘트는 다음과 같다. 모두 각 조각의 도심에 대한 단면의 2차 모멘트이다. 윗첨자 $L$은 local을 의미한다.
\begin{align} I_{z1}^L &= \frac{b_1t_1^3}{12} \\\\ I_{z2}^L &= \frac{t_2b_2^3}{12} \\\\ I_{z3}^L &= \frac{b_3t_3^3}{12} \end{align}
위 식은 각 도심에 대해 구한 것이므로 기준이 제각각이다. 이 값들을 전체 도심에 대해 평행 축 이동 정리를 적용하여 모두 더하면 전체 형강의 단면 2차 모멘트를 구할 수 있다.
\begin{align} I_{z1} &= I_{z1}^L + A_1(\bar{y_1}-\bar{y})^2 \\\\ I_{z2} &= I_{z2}^L + A_1(\bar{y_2}-\bar{y})^2 \\\\ I_{z3} &= I_{z3}^L + A_1(\bar{y_3}-\bar{y})^2 \end{align}
$$ \therefore I_z = I_{z1} + I_{z2} + I_{z2} $$
기준을 먼저 통일한 후 구하는 방법도 생각해볼 수 있다. 각 조각들을 $z'$축에 대해 평행 축 이동하여 기준을 일치 시킨 뒤 모두 더해 $z'$ 축에 대한 전체 단면의 2차 모멘트를 구한다. 그리고 다시 전체 단면의 도심에 대해 평행축 이동하는 방법이다.
1) $z'$ 축에 대해 각 조각을 평행축 이동한다.
\begin{align} I_{z1'} &= I_{z1}^L + A_1\bar{y_1}^2 \\\\ I_{z2'} &= I_{z2}^L + A_2\bar{y_2}^2 \\\\ I_{z3'} &= I_{z3}^L + A_3\bar{y_3}^2 \end{align}
2) $z'$ 축에 대한 전체 단면의 2차 모멘트를 구한다.
$$ I_{z'} = I_{z1'} + I_{z1'} +I_{z1'} $$
3) 전체 단면의 도심에 대해 반대로 평행 축 이동한다.
$$ I_z = I_{z'} - A\bar{y}^2 $$




최근댓글