1. 박판 압력 용기
박판 압력 용기는 면의 치수에 비해 두께가 아주 얇은 형태의 구조물로써 내부에 고압의 유체를 보관하는 용도로 사용한다. 흔히 볼 수 있는 부탄 가스통, LPG 탱크, 질소 탱크, 또는 LNG 선박에 있는 둥그런 탱크들이 이런 박판 압력 용기에 해당한다. 유체의 압력은 어디에서나 같기 때문에 용기 내벽에는 동일한 크기의 압력이 작용하게 된다. 이러한 박판 용기는 원통형(cylindrical)이나 구형(spherical)또는 반구형(hemispherical)으로 3차원 구조물이지만 두께가 얇기 때문에 평면 응력 상태(plane stress state)로 가정할 수 있다.
$$ \frac{r}{t} > 10 \\\\ \text{where, t: thickness, r: inner radius} $$
실제로는 두께 방향 응력에 구배가 있지만 두께가 얇아 전체적으로 거의 차이가 없어 전 두께에 걸쳐 평균 응력이 균일하게 작용한다고 본다.
$$ \frac{\sigma_{\text{max}} - \sigma_{\text{avg}}}{\sigma_{\text{max}}} < 0.04 $$

2. 원통형 압력 용기
원통형 압력 용기의 단면을 그림 2에 나타냈다.
\begin{align} t&:\ \text{thickness} \\\\ r&:\ \text{inner radius of cylinder} \\\\ p&:\text{internal pressure} \end{align}
\begin{align} \sigma_1&:\ \text{circumferential or hoop stress} \\\\ \sigma_2&:\ \text{longitudinal or axial stress} \end{align}

2.1. 원주 응력 (Hoop Stress)

가로 방향으로 원통을 잘라서 상태를 보면 그림 3과 같다. 곡률이 있는 원통면에 작용하는 압력은 양 옆으로 작용하는 성분은 서로 상쇄되어 사라지고 아래 방향으로 작용하는 성분만 의미 있을 것이다. 이것은 원통면을 정사영(projection)한 면적에 압력이 작용하는 것으로 볼 수 있다. 압력과 미소 면적의 법선 벡터가 이루는 내적에서 압력에 $\cos$을 곱하나 면적에 곱하나 마찬가지 결과를 주기 때문이다.
$$ (p\cos\theta)dA = pdA\cos\theta $$
원기둥형 원통의 길이를 L이라고 하면,
$$ \sum{F_V} = \sigma_12(tL) - p(2r)L = 0 \\\\ \therefore \sigma_1 = \frac{pr}{t} $$
2.2. 축방향 응력 (Axial Stress)

세로 방향으로 원통을 잘라서 상태를 보면 그림 4와 같다. 곡률이 있는 옆면에 작용하는 압력 역시 정사영 면적에 작용하는 것으로 생각할 수 있다. 따라서 곡률이 있으나 없으나 계산에는 상관이 없다.
$$ sum{F_H} = -p\pi r^2 + \sigma_2(2\pi rt) = 0 \\\\ \therefore \sigma_2 = \frac{pr}{2t} $$
축 방향 응력은 원주 방향 응력의 절반이라는 것을 알 수 있다. 따라서 용접을 통해 원통형 내압 용기를 만든다면 원주방향이 축 방향보다 두 배 더 큰 하중을 견디도록 설계해야 한다.
$$ \therefore \sigma_1 = 2\sigma_2 $$
2.3. 파손 이론
원통형 압력용기를 강판을 용접해서 만든다면 연성재의 파손이므로 최대 전단 응력에 의해 파손될 것이라고 생각할 수 있다. 이것이 Tresca 항복 조건(Tresca's yielding condition)이다.
\begin{align} \sigma_1 &= \frac{pr}{t} \\\\ \sigma_2 &= \frac{pr}{2t} \\\\ \sigma_3 &= -p \approx 0 \end{align}
박판 압력 용기는 축 방향과 원주 방향으로 이루어진 좌표계에서는 전단 응력이 존재하지 않으므로 순수 인장 상태가 되어 주응력 방향이 된다. 따라서 최대 전단 응력은 주응력과의 관계를 이용하여 구할 수 있다.
\begin{align} \tau_1 &= \frac{1}{2}|\sigma_2 - \sigma_3| \\\\ \tau_2 &= \frac{1}{2}|\sigma_1-\sigma_3| \\\\ \sigma_3 &= \frac{1}{2}|\sigma_1 - \sigma_2| \end{align}
$$ \therefore \tau_{\text{max}} = \tau_2 = \frac{\sigma_1}{2} = \frac{pr}{2t} $$
3. 구형 압력 용기
구형 압력 용기의 중심을 지나도록 분할한 단면을 그림 5에 나타냈다.

3.1. 자오 응력 (Meridional Stress)
분할면이 중심이 지나기만 하면 어떤 각도로 잘라도 항상 같은 결과를 얻을 수 있다. 따라서 $\sigma_1$과 $\sigma_2$는 같고 모든 회전된 좌표계의 응력 상태는 동일하다. 이 응력 방향은 구껍질에서 항상 자오선을 향하므로 자오 응력(meridional stress)이라고 한다.
$$ \sigma = \sigma_m = \sigma_1 = \sigma_2 $$
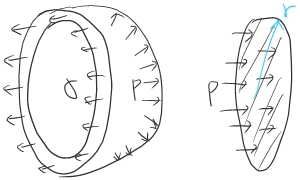
그림 6을 평형 방정식을 이용해 풀어보면 다음과 같다.
$$ \sum{F} = p\pi r^2 - \sigma(2\pi rt) = 0 \\\\ \therefore \sigma = \frac{pr}{2t} $$
3.2. 파손 이론
원통형과 마찬가지로 연성재일 때 Tresca 파손 이론을 적용하여 최대 전단 응력이 전단 강도에 도달할 때 파손이 일어난다고 볼 수 있다. 최대 전단 응력은 다음과 같다.
$$ \tau_{\text{max}} = \frac{1}{2}|\sigma_1 - \sigma_3| = \frac{pr}{4t} $$
4. Filament Winding
항공우주용 내압 용기는 필라멘트 와인딩 방식으로 제작하는 경우가 많다. 이것은 복합재를 이용한 방법으로 무게는 작으면서 강성과 강도는 높은 내압 용기를 제작할 수 있기 때문이다. 단방향 복합재는 섬유 방향으로는 강도가 크지만 섬유 방향과 90도가 되는 방향은 수지가 힘을 버티기 때문에 강도가 작다. 따라서 원통형 용기를 만들 때 원주 방향과 섬유 방향이 완전히 일치하도록 감으면 원주 응력에는 잘 버틸 수 있으나 축방향 응력에는 취약하게 된다. 따라서 실패(fail 아님)에 실을 감듯이 사선으로 감아 강도를 배분한다. 이렇게 섬유를 감는 각도를 조절해 원주 방향과 축 방향 강도를 조절할 수 있다.

그림 7과 같은 구조에서 섬유 방향 응력을 복합재의 0도 방향 응력 $\sigma_0$이라고 하면 아래와 같이 원주 응력과 축 방향 응력을 구할 수 있다. 보통 복합재의 경우 0도 방향을 섬유 방향으로 한다.
\begin{align} F_1 &= F_{\theta}\sin\theta \\\\ F_2 &= F_{\theta}\cos\theta \\\\ F_{\theta} &= \sigma_0bt \end{align}
이제 그림 8을 참고해 원주 응력과 축 방향 응력을 구해보자.

\begin{align} \sigma_1 &= \frac{F_1}{A_1} = \frac{F_{\theta}\sin\theta}{b_1t} = \frac{F_{\theta}}{bt}\sin^2\theta \\\\ &= \sigma_0bt\cdot\frac{\sin^2\theta}{bt} = \sigma_0\sin^2\theta \\\\ \sigma_2 &= \frac{F_2}{A_2} = \frac{F_{\theta}\cos\theta}{b_2t} = \frac{F_{\theta}}{bt}\cos^2\theta \\\\ &= \sigma_0bt\cdot\frac{\cos^2\theta}{bt} = \sigma_0\cos^2\theta \end{align}
따라서 내압에 의한 응력은 아래와 같다.
\begin{align} \sigma_1 &= \frac{pr}{t} = \sigma_0\sin^2\theta \\\\ \sigma_2 &= \frac{pr}{2t} = \sigma_0\cos^2\theta \end{align}
$$ \therefore \frac{pr}{\sigma_0t} = \sin^2\theta = 2\cos^2\theta $$
각도 $\theta$에 대한 탄젠트 제곱은 항상 2가 된다.
$$ \tan^2\theta = \frac{\sigma_0\sin^2\theta}{\sigma_0\cos^2\theta} = 2 $$




최근댓글