1. 스트레인 게이지 (Strain Gauge)
우리는 물리학 시간에 도선의 저항은 길이에 비례하고 단면적에 반비례한다는 것을 배웠다.
$$ R \propto \frac{L}{A} $$
여기에 비례 상수 $\rho$를 도입하면,
$$ R = \frac{\rho L}{A} $$
변형률의 측정에는 이런 저항의 변화를 이용한다. 도선을 어떤 물체에 붙여 놓고 물체가 늘어나면 도선도 같이 늘어나게 되어 저항이 늘어나는 원리를 이용하는 것이다. 이때 길이가 늘어나면서 단면적도 줄어들게 되는데 이것 역시 저항을 증가시킨다. 이제 도선 재료의 비례 상수 $\rho$를 알고 변형에 대한 저항 변화의 민감도(sensitivity)를 알면 저항을 측정해 변형률을 알 수 있게 된다.
$$ \frac{\Delta R}{R} = GF \frac{\Delta L}{L} = GF\epsilon $$
위 식에서 GF는 게이지 인자(gauge factor)이고 금속 재료는 체적 불변을 가정하면 항상 2가 된다. 물론 실제 금속재는 비압축성이 아니기 때문에 체적 불변이 아니므로 2에 가까운 값을 갖게 될 것이다.
심심하니까 GF가 왜 2가 되는지 구해보자. 먼저 우리가 알고 싶은 것은 길이 변화에 대한 저항의 변화이다. 따라서 저항에 대한 길이와 단면적의 비례식을 길이 $L$로 미분해 본다. 여기서 주의할 점은 길이 L과 단면적 A는 서로 독립이 아니고 $A=A(L)$이 된다. 길이가 변하면 단면적이 변하기 때문이다. 이 관계는 체적은 변하지 않는다는 말도 안 되는 가정으로 퉁치고 넘어간다.
체적은 다음과 같다.
$$ V = AL $$
따라서 $V$는 상수이고 다시 아래처럼 쓸 수 있다.
$$ A = \frac{V}{L} $$
따라서 길이 변화에 따른 면적의 변화는 면적 $A$를 길이 $L$로 미분하여,
\begin{align} \frac{dA}{dL} &= \frac{dV}{dL}\cdot L - \frac{V}{L^2} \\\\ &= -\frac{AL}{L^2} \\\\ &= -\frac{A}{L} \end{align}
이제 길이 변화에 대한 저항의 변화를 구하기 위해 저항 $R$을 길이 $L$로 미분한다.
\begin{align} R &= \frac{\rho L}{A} \\\\ \frac{dR}{dL} &= \frac{\partial R}{\partial L}\frac{dL}{dL} + \frac{\partial R}{\partial A}\frac{dA}{dL} \\\\ &= \frac{\partial R}{\partial L} + \frac{\partial R}{\partial A}\frac{dA}{dL} \\\\ &= \frac{\rho}{A} + \left(-\frac{\rho L}{A^2}\right)\left(-\frac{A}{L}\right) \\\\ &= \frac{2\rho}{A} \\\\ &= 2\cdot\frac{R}{L} \end{align}
위 식을 정리하면 GF는 항상 2가 된다.
$$ \frac{dR/R}{dL/L} = 2 $$
변형률은 저항에 비례한다는 것을 알 았으니 변형률을 알기 위해 대신 저항의 변화 $\Delta R$을 계측해도 마음이 편안하다. 이때 저항의 변화가 클수록 즉 잡음(noise) 대비 신호의 강도가 높아져 측정이 용이하다. 따라서 스트레인 게이지는 아래처럼 구불구불하게 도선을 여러 번 겹쳐서 작은 면적에 긴 도선이 들어가도록 한다. 변형을 측정하고 싶은 방향을 도선의 긴 방향에 맞춰서 붙이면 된다.
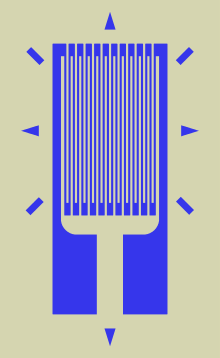
하지만 실제로 이렇게 생긴 단순한 스트레인 게이지를 쓰면 아주 작은 미소 변형을 다루는 고체역학의 변형을 측정하기는 어렵다. 따라서 휘트스톤 브리지(wheatstone bridge) 형태의 회로를 이용해 감도를 높이고 열팽창에 의해 늘어나는 효과를 없앨 수 있다. 물론 기본 원리는 같다.

2. 측정 결과의 계산
스트레인 게이지를 구매하게 되면 구불구불한 도선이 들어간 패치 형태로 되어 있음을 알 수 있다. 이 하나의 패치에 게이지가 한 개만 있는 것을 1축 게이지라고 한다. 이런 게이지는 한 방향의 변형률만 측정할 수 있다.
포아송 비까지 구하고자 하면 스트레인 게이지를 직각으로 두 개 붙여야 한다. 포아송 비는 추후에 다루겠지만 종방향 변형이 발생했을 횡방향이 얼마나 줄어드는지를 알려주는 비율이다. 길이가 늘어날 때 단면적이 줄어드는 것을 말하는 것이다.
$$ \nu = -\frac{\epsilon_y}{\epsilon_x} $$
스트레인 게이지가 3개 있으면 한 방향 $\epsilon_x$와 90도 회전한 방향 $\epsilon_y$, 그리고 전단 변형 $\gamma_{xy}$까지 모두 구할 수 있다. 아래 세 개의 식을 이용해 연립 방정식을 풀어 구할 수 있기 때문이다.
\begin{align} \epsilon_a &= \epsilon_x\cos^2{\theta_a} + \epsilon_y\sin^2{\theta_a} +\gamma_{xy}\cos{\theta_a}\sin{\theta_a} \\\\ \epsilon_b &= \epsilon_x\sin^2{\theta_b} + \epsilon_y\cos^2{\theta_b} -\gamma_{xy}\sin{\theta_b}\cos{\theta_b} \\\\ \epsilon_c &= \epsilon_x\sin^2{\theta_c} + \epsilon_y\cos^2{\theta_c} -\gamma_{xy}\sin{\theta_c}\cos{\theta_c} \end{align}

3. 스트레인 로제트 (Strain Rosette)
모든 변형을 알기 위해서는 1축 게이지를 세 개나 붙여야 한다. 이때 각 게이지 사이의 각도를 정확하게 알지 않으면 계산 결과에 오차로 나타나게 된다. 이런 수고로움을 덜기 위해 아예 3축 게이지가 하나의 패치에 들어있는 스트레인 로제트를 쓰면 편리하다. 좀 더 비싸지만 여러분의 인건비도 돈이다! 스트레인 로제트는 45도 간격으로 구성된 rectanguar rosette와 60도 간격으로 구성된 delta rosette가 주로 쓰인다.
3.1. Rectangular Rosette (45˚)
Rectangular Rosette는 세 개의 스트레인 게이지를 45도 간격으로 배치하고 스트레인 게이지의 연장선이 만나는 점을 측정점으로 간주한다.

각 게이지의 측정 결과는 아래와 같은 의미를 갖는다.
\begin{align} \epsilon_{0^\circ} &= \epsilon_x \\\\ \epsilon_{90^\circ} &= \epsilon_y \\\\ \epsilon_{45^\circ} &= \epsilon_x\cos^2{45^\circ}+\epsilon_y\sin^2{45^\circ} + \gamma_{xy}\cos45^\circ\sin45^\circ \\\\ &= \frac{1}{2}(\epsilon_x + \epsilon_y + \gamma_{xy}) \end{align}
따라서 다음과 같이 변형률 상태를 구할 수 있다.
\begin{align} \epsilon_x &= \epsilon_{0^\circ} \\\\ \epsilon_y &= \epsilon_{90^\circ} \\\\ \gamma_{xy} &= 2\epsilon_{45^\circ} - \epsilon_{0^\circ} - \epsilon_{90^\circ} \end{align}
3.2. Delta Rosette (60˚)
Delta Rosette는 60도 간격 정삼각형으로 스트레인 게이지를 배치하고 도심의 위치를 측정점으로 간주한다. 측정점이 스트레인 게이지가 늘어나는 방향과 완전히 일치하지 않지만 거의 비슷하다고 본다. 이게 싫어서 방사형으로 60도 간격으로 배열한 로제트도 있다.

각 게이지의 측정 결과는 다음과 같은 의미를 갖는다.
\begin{align} \epsilon_{0^\circ} &= \epsilon_x \\\\ \epsilon_{60^\circ} &= \epsilon_x\cos^2{60^\circ} + \epsilon_y\sin^2{60^\circ} + \gamma_{xy}\cos{60^\circ}\sin{60^\circ} \\\\ &= \frac{1}{4}\epsilon_x + \frac{3}{4}\epsilon_y + \frac{\sqrt{3}}{4}\gamma_{xy} \\\\ \epsilon_{120^\circ} &= \epsilon_x\cos^2{120^\circ} + \epsilon_y\sin^2{120^\circ} + \gamma_{xy}\cos{120^\circ}\sin{120^\circ} \\\\ &= \frac{1}{4}\epsilon_x + \frac{3}{4}\epsilon_y - \frac{\sqrt{3}}{4}\gamma_{xy} \end{align}
위 식에서 $$epsilon_{60^\circ}$와 $\epsilon_{120^\circ}$를 더하고 빼면 아래와 같은 관계식을 얻는다.
\begin{align} \epsilon_{60^\circ} + \epsilon_{120^\circ} &= \frac{1}{2}\epsilon_x + \frac{3}{2}\epsilon_y \\\\ \epsilon_{60^\circ} - \epsilon_{120^\circ} &= \frac{\sqrt{3}}{2}\gamma_{xy} \end{align}
정리하면 아래와 같이 변형률 상태를 구할 수 있다.
\begin{align} \epsilon_x &= \epsilon_{0^\circ} \\\\ \epsilon_y &= \frac{1}{3}(2\epsilon_{60^\circ} + 2\epsilon_{120^\circ} - \epsilon_{0^\circ} \\\\ \gamma_{xy}) &= \frac{2}{\sqrt{3}}(\epsilon_{60^\circ}-\epsilon_{120^\circ}) \end{align}




최근댓글