1. 평면 변형률 (Plane Strain)
잠시 평면 응력(plane stress)을 다시 생각해보자. 평면 응력 상태는 의미 있는 응력 성분이 하나의 평면 상에 존재하는 상태를 말한다. 예를 들어 두께가 얇은 경우에는 면외 저항을 거의 하지 않기 때문에 두께 방향으로 상대 변위가 거의 없다. 따라서 두께 방향 응력이 아주 작게 되어 $\sigma_z = 0$으로 취급하고 2차원 응력 상태로 다룰 수 있게 된다.
$$ \sigma_z = 0,\quad \tau_{xz} = 0,\quad \tau_{yz} = 0 $$
$$ \begin{bmatrix} \sigma \end{bmatrix} = \begin{bmatrix} \sigma_{x} & \tau_{xy} & \tau_{xz} \\ \tau_{yx} & \sigma_y & \tau_{yz} \\ \tau_{zx} & \tau_{zy} & \sigma_z \end{bmatrix} = \begin{bmatrix} \sigma_{x} & \tau_{xy} & 0 \\ \tau_{yx} & \sigma_y & 0 \\ 0 & 0 & 0 \end{bmatrix} \Rightarrow \begin{bmatrix} \sigma_{x} & \tau_{xy} \\ \tau_{yx} & \sigma_y \end{bmatrix} $$
평면 변형률도 평면 응력과 얼핏 비슷해 보인다. 하지만 반대로 평면 변형률은 두께가 아주 두꺼울 때 두께 방향 변형률을 무시할 수 있는 경우이다. 고체역학에서는 미소 변형을 다루므로 변형이 아주 작은데 여기에다 두께 $t$가 아주 두꺼우면 수직 변형률은 거의 0에 가깝게 될 것이다.
$$ \epsilon_z = \lim_{t\rightarrow\infty} \frac{\delta_z}{t} = 0 $$
그리고 두께 방향으로 변위의 구배(gradient)가 널리 퍼져 매우 작으면 전단 변형률 역시 0으로 취급할 수 있다.
$$ \gamma_{xz} = \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x} = 0 $$
$$ \gamma_{yz} = \frac{\partial v}{\partial z} + \frac{\partial w}{\partial y} = 0 $$
따라서 평면 변형률은 두께 방향의 변형률을 무시하여 2차원 변형률 상태로 취급한다.
$$ \epsilon_z = 0,\quad \gamma_{xz} = 0,\quad \gamma_{yz} = 0 $$
$$ \begin{bmatrix} \epsilon \end{bmatrix} = \begin{bmatrix} \epsilon_{x} & \gamma_{xy} & \gamma_{xz} \\ \gamma_{yx} & \epsilon_y & \gamma_{yz} \\ \gamma_{zx} & \gamma_{zy} & \epsilon_z \end{bmatrix} = \begin{bmatrix} \epsilon_{x} & \gamma_{xy} & 0 \\ \gamma_{yx} & \epsilon_y & 0 \\ 0 & 0 & 0 \end{bmatrix} \Rightarrow \begin{bmatrix} \epsilon_{x} & \gamma_{xy} \\ \gamma_{yx} & \epsilon_y \end{bmatrix} $$
2. 어따 쓰나?
평면 응력이나 평면 변형률 상태로 가정하면 3차원 문제를 2차원 문제로 축소하여 수학적인 간결함을 얻을 수 있다.
예를 들어 아래 그림 1의 긴 파이프의 단면은 평면 변형률 상태로 다룰 수 있다.

압출 성형으로 만든 부재는 길이 방향으로 동일한 단면을 갖는다. 대표적으로 알루미늄 프로파일(aluminum profile)을 구조재로 많이 사용하는데 이러한 부재를 분석할 때도 평면 변형률 상태로 다룰 수 있다.

아래 그림 3과 같은 긴 댐(dam) 구조물은 평면 변형률의 단골 예시이다. 이런 구조물은 단면을 취해 평면 변형률 상태로 취급할 수 있다. 거대한 전체 구조물을 다루기보다 단면을 다루는 편이 간단할 것이다.

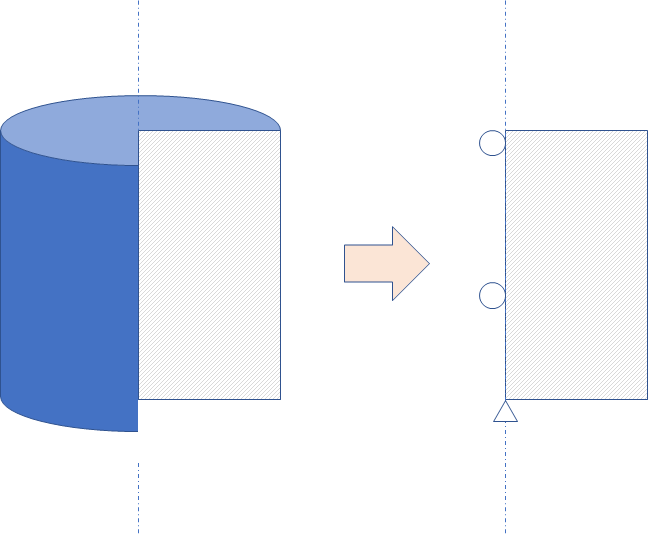
축대칭(axisymmetric) 구조물도 실린더 좌표계에서 보면 평면 변형률 상태와 같다.
3. 주의할 점
평면 응력 상태에서 두께 방향 응력이 없다고 해서 두께 방향 변형도 없는 것은 아니었다. 마찬가지로 평면 변형률 상태에서 두께 방향 변형률이 없더라도 두께 방향 응력은 존재하게 된다. 이것 역시 포아송 비(Poisson's ratio)에 의해 면내 변형률 성분이 면외 방향 응력에 영향을 주는 것이다.
$$ \begin{align} \begin{bmatrix} \sigma \end{bmatrix} &= \begin{bmatrix} \sigma_{x} & \tau_{xy} & 0 \\ \tau_{yx} & \sigma_y & 0 \\ 0 & 0 & \sigma_z \end{bmatrix} \\\\ \begin{bmatrix} \epsilon \end{bmatrix} &= \begin{bmatrix} \epsilon_{x} & \gamma_{xy} & 0 \\ \gamma_{yx} & \epsilon_y & 0 \\ 0 & 0 & 0 \end{bmatrix} \end{align} $$
여기에서 $\sigma_z$는 구성방정식(constitutive equation)을 통해 다음과 같이 구한다. 자세한 내용은 추후에 다시 다루도록 한다.
$$ \sigma_z = \frac{E}{(1+\nu)(1-2\nu)}\left[ (1-\nu)\epsilon_z + \nu(\epsilon_x + \epsilon_y) \right] $$




최근댓글