1. 모어 원(Mohr's Circle)
모어 원은 응력 변환(stress transformation)의 도식법(graphical method)이다. 회전된 좌표계에 대한 응력 성분을 구할 때 변환 공식을 이용하는 대신 간단하게 원을 몇 개 그려서 구할 수 있는 방법이다. 1800년대에 Otto Mohr라는 독일의 철도기사가 좌표에 따른 응력의 변환을 도식적으로 구하는 방법에 대해 연구한 것으로 이 공로를 인정받아 독일 명문 Stuttgart 공과대학 교수로 초빙되었다. 이때 그의 나이 무려 23세였다. 젊은 나이에 교수가 되는 것도 대단하지만 철도 기사가 교수가 되는 독일 사회도 놀라울 뿐이다.
\begin{align} \sigma_x' &= \frac{1}{2}(\sigma_x+\sigma_y) + \frac{1}{2}(\sigma_x-\sigma_y)\cos2\theta + \tau_{xy}\sin2\theta \\\\ \tau_{x'y'} &= -\frac{1}{2}(\sigma_x-\sigma_y)\sin2\theta + \tau_{xy}\cos2\theta \end{align}
2. 응력 원(Stress Circle)
위에 있는 응력 변환 공식을 가만히 보고 있자니 뭔가 공통된 부분들이 보인다. 수직 응력식을 살짝 바꿔서 아래처럼 써보면 더 눈에 잘 보이게 된다.
\begin{align} \sigma_x' - \frac{1}{2}(\sigma_x+\sigma_y) &= \frac{1}{2}(\sigma_x-\sigma_y)\cos2\theta + \tau_{xy}\sin2\theta \\\\ \tau_{x'y'} &= -\frac{1}{2}(\sigma_x-\sigma_y)\sin2\theta + \tau_{xy}\cos2\theta \end{align}
이제 두 식 양변을 제곱한다.
\begin{align} \left[\sigma_x' - \frac{1}{2}(\sigma_x+\sigma_y)\right]^2 &= \frac{1}{4}(\sigma_x-\sigma_y)^2\cos^2{2\theta} + \tau_{xy}^2\sin^2{2\theta} + \frac{1}{2}(\sigma_x-\sigma_y)\tau_{xy}\cos2\theta\sin2\theta \\\\ \tau_{x'y'}^2 &= \frac{1}{4}(\sigma_x-\sigma_y)^2\sin^2{2\theta} + \tau_{xy}^2\cos^2{2\theta} -\frac{1}{2}(\sigma_x-\sigma_y)\tau_{xy}\cos2\theta\sin2\theta \end{align}
두 식을 더 한다.
\begin{align} \left[\sigma_x' - \frac{1}{2}(\sigma_x+\sigma_y)\right]^2 + \tau_{x'y'}^2 = &\frac{1}{4}(\sigma_x-\sigma_y)^2(\cos^2{2\theta} + \sin^2{2\theta}) \\\\ &+ \tau_{xy}^2(\cos^2{2\theta} + \sin^2{2\theta}) \end{align}
여기에서 $\cos^2{2\theta} + \sin^2{2\theta} = 1$이므로 정리하면 아래와 같다.
$$ \left[\sigma_x' - \frac{1}{2}(\sigma_x+\sigma_y)\right]^2 + \tau_{x'y'}^2 = \frac{1}{4}(\sigma_x-\sigma_y)^2 + \tau_{xy}^2 $$
이제 다음과 같이 변환된 수직 응력과 전단 응력을 변수로 생각하고 복잡해 보이는 식을 간단하게 치환해보자.
\begin{align} &\sigma_x' \Rightarrow \sigma \\\\ & \tau_{x'y'} \Rightarrow \tau \\\\ &\frac{1}{2}(\sigma_x + \sigma_y) = \sigma_{\text{av}} \\\\ &\frac{1}{4}(\sigma_x-\sigma_y)^2 + \tau_{xy}^2 = r^2 \end{align}
결과적으로 식은 다음과 같이 익숙한 원의 방정식 형태로 간단하게 정리된다. 이것을 응력 원(stress circle)이라고 한다.
$$ (\sigma-\sigma_{\text{av}})^2 + \tau^2 = r^2 $$

3. 모어 원 그리는 방법(Construction Method of Mohr's Circle)
모어 원을 그리는 이유는 이미 알고 있는 응력 상태를 이용해 주응력과 주평면, 그리고 최대 전단 응력과 최대 전단 응력 평면을 쉽게 구할 수 있기 때문이다.
$$ \sigma_x, \ \sigma_y, \ \tau_{xy} \Rightarrow \sigma_1,\ \sigma_2,\ \theta_p,\ \tau_{\text{max}},\ \theta_s $$
주어진 응력 상태로 평균 수직 응력을 중심으로하는 원을 그리면 아래 그림 2와 같다.
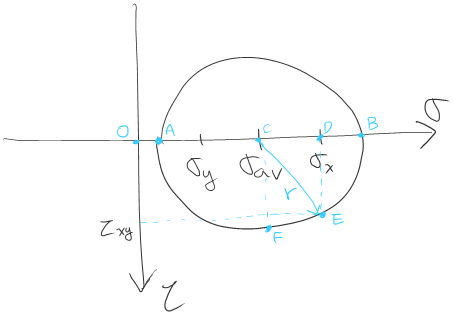
먼저 $\sigma$축과 $\tau$ 축을 그린다. $\tau$의 방향이 반대인 점에 유의 한다. Beer책으로 공부한 사람들은 $\tau$축을 위로 올라가는 방향으로 그릴 텐데 어떤 방법으로 하던지 여러분의 마음이다.
현재 좌표계에서의 응력 성분 $\sigma_x,\ \sigma_y$를 각각 표시하고 그 평균인 $\sigma_{\text{av}}$를 표시한다. 이 평균 수직 응력이 모어 원의 중심이 된다.
그다음 그래프 위 $(\sigma_x, \tau_{xy})$의 위치에 점을 찍고(E점) 원의 중심과 선을 이은 뒤 이 선을 반경으로 하는 원을 그린다.
그려진 원은 그림 2와 같다. 이 원에서 A점은 최소 주응력 $\sigma_2$을 의미한다. B점은 최대 주응력 $\sigma_1$을 의미한다. 마찬가지로 F점은 $\tau$ 축에서 최대이므로 $\tau_{\text{max}}$를 의미한다는 것을 알 수 있다.
그림 2에서 선분들의 길이는 아래 관계를 갖는다.
\begin{align} \overline{OC} &= \sigma_{\text{av}} \\\\ \overline{CD} &= \overline{OD} - \overline{OC} \\\\ &= \sigma_x - \frac{1}{2}\sigma_{\text{av}} \\\\ &= \frac{1}{2}(\sigma_x - \sigma_y) \\\\ \overline{OA} &= \overline{OC} - r \\\\ &= \frac{1}{2}(\sigma_x+\sigma_y) - r \\\\ &= \frac{1}{2}(\sigma_x+\sigma_y) -\sqrt{\frac{1}{4}(\sigma_x-\sigma_y)^2 + \tau_{xy}^2} = \sigma_2 \\\\ \overline{OB} &= \overline{OC} + r \\\\ &= \frac{1}{2} (\sigma_x+\sigma_y) + r \\\\ &= \frac{1}{2}(\sigma_x+\sigma_y) +\sqrt{\frac{1}{4}(\sigma_x-\sigma_y)^2 + \tau_{xy}^2} = \sigma_1 \\\\ \overline{CF} &= r \\\\ &= \sqrt{\frac{1}{4}(\sigma_x-\sigma_y)^2 + \tau_{xy}^2} = \tau_{\text{max}} \end{align}
주평면과 최대 전단 응력 평면의 각도는 아래 그림 3처럼 찾을 수 있다.
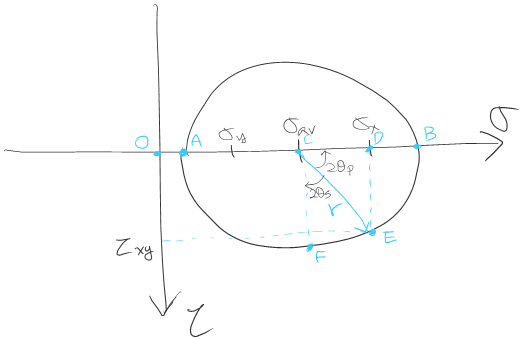
그림 3에 나타난 선분들의 각도는 다음 관계를 갖는다.
\begin{align} \tan\angle{DCE} &= \frac{\overline{DE}}{\overline{CD}} \\\\ &= \frac{\tau_{xy}}{\frac{1}{2}(\sigma_x - \sigma_y)} \\\\ &= \frac{2\tau_{xy}}{\sigma_x-\sigma_y} = \tan2\theta_p \\\\ \tan(-\angle{ECF}) &= -\tan\angle{ECF} \\\\ &= -\frac{\overline{CD}}{\tau_{xy}} \\\\ &= -\frac{\sigma_x-\sigma_y}{2\tau_{xy}} = \tan2\theta_s \end{align}




최근댓글