1. 응력 성분의 표기법
한 점에 여러 가지 응력이 동시에 작용할 경우 각각의 응력 성분을 구분하기 위한 표기법을 설명한다. 기본적인 표기법은 아래 첨자 두 개를 사용하는 것이며 아래 그림 1에 표기했다.
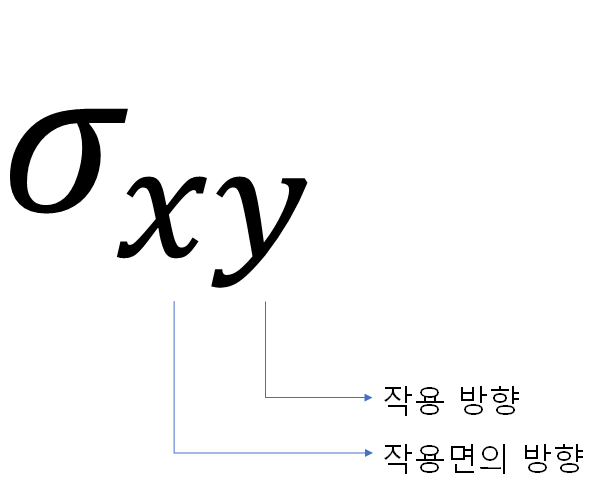
1.1. 수직 응력
$\sigma_{xy}$에서 $x$는 작용면을 의미한다. 그리고 $y$는 내력이 작용하는 방향이다. 수직 응력은 평면의 수직 방향(normal direction)과 작용 방향이 일치해 같은 문자를 두 번 쓰게 되므로 편의를 위해 한 번만 쓰기도 한다. 공돌이의 기본은 늘 가정과 생략이다.
- $\sigma_{xx} = \sigma_x$: $x$평면에 $x$방향으로 작용하는 수직 응력
- $\sigma_{yy} = \sigma_y$: $y$평면에 $y$방향으로 작용하는 수직 응력
- $\sigma_{zz} = \sigma_z$: $z$평면에 $z$방향으로 작용하는 수직 응력
수직 응력이 작용하면 그림 2처럼 길이, 면적, 체적이 변한다.

1.2. 전단 응력
모든 응력에 대해서 $\sigma$로 표현해도 되지만 구분의 편의를 위해 전단 응력은 $\tau$로 별도 표기하기로 한다.아래 첨자의 의미는 늘 동일하다.
- $\sigma_{xy} = \tau_{xy}$: $x$평면에 $y$방향으로 작용하는 전단 응력
- $\sigma_{xz} = \tau_{xz}$: $x$평면에 $z$방향으로 작용하는 전단 응력
- $\sigma_{yx} = \tau_{yx}$: $y$평면에 $x$방향으로 작용하는 전단 응력
- $\sigma_{yz} = \tau_{yz}$: $y$평면에 $z$방향으로 작용하는 전단 응력
- $\sigma_{zx} = \tau_{zx}$: $z$평면에 $x$방향으로 작용하는 전단 응력
- $\sigma_{zy} = \tau_{zy}$: $z$평면에 $y$방향으로 작용하는 전단 응력
전단 응력은 길이, 면적, 체적에 변화를 주지 않고 형상의 변화를 야기한다. 형상의 변화는 각도가 바뀌는 것을 말한다.

2. 부호 규약 (Sign Convention)
응력의 방향은 내력의 방향과 같다. 평면의 외향 수직 벡터(outward normal vector)가 응력의 양의 방향이 된다. 평면이 방향이 음이 방향이면 이 방향이 응력의 양의 방향이 되는 것이다.
2.1. 2차원 응력
2차원 문제에서 응력의 방향을 그림 2에 도시했다. 그림 2에서 $-x$ 평면에 작용하고 있는 $\sigma_x$를 보자. 이 평면의 외향 수직 벡터는 음의 방향이지만 이 방향이 수직 응력 $\sigma_x$의 양의 방향이 된다. 마찬가지로 $-x$ 평면에 작용하는 전단 응력 $\tau_{xy}$도 $-x$평면이 음의 방향이므로 $-y$이 양의 방향이 되는 것이다. 쉽죠?

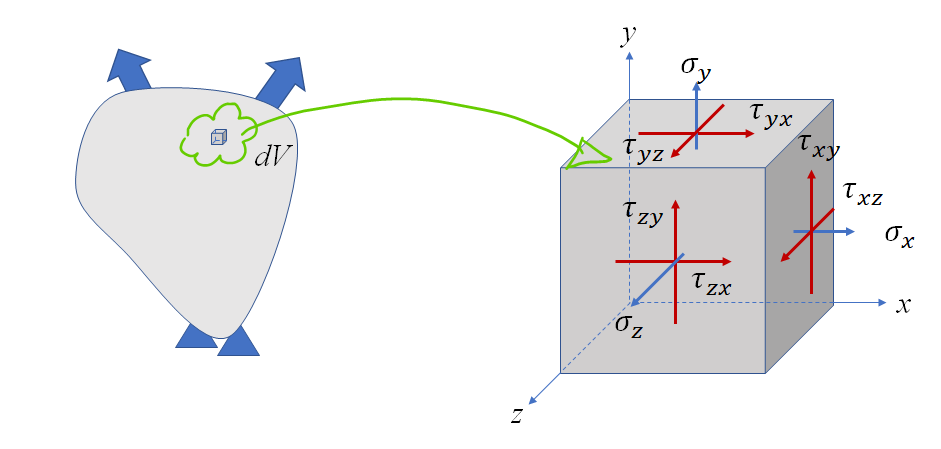
2.2 3차원 응력
3차원 응력도 2차원 응력과 동일하게 표현한다.
3. 외팔보 예제
반력을 구할 때 봤던 외팔보에 작용하는 응력을 구해보자. 외팔보의 단면적은 모든 길이 $L$에 대해 $A$로 일정하다.

외력의 평형 방정식을 세운다.
\begin{align} \sum{F_x} &= A_x -P\cos{\theta} = 0 \\\\ \sum{F_y} &= A_y + -P\sin{\theta} = 0 \\\\ \sum{M_z|_A} &= M_A -P\sin{\theta}L= 0 \end{align}
반력은 아래와 같이 결정 된다.
\begin{align} A_x &= P\cos{\theta} \\\\ A_y &= P\sin{\theta} \\\\ M_A &= PL\sin{\theta} \end{align}
분할법을 이용해 $a$점에서의 내력을 표시한다.
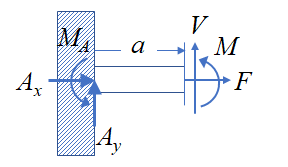
내력의 평형 방정식을 세운다. 모멘트의 평형 방정식을 세울 때 미지수가 많은 곳을 기점으로 하면 식에 미지수가 사라져 계산이 편리하다. A점에서 세우면 미지수 $V$가 살아나 계산이 조금 피곤해질 수 있다.
\begin{align} \sum{F_x} &= A_x + F = 0 \\\\ \sum{F_y} &= A_y + V = 0 \\\\ \sum{M_z|_a} &= M_A + M - A_ya = 0 \end{align}
내력은 다음과 같이 결정된다.
\begin{align} F &= -A_x = -P\cos{\theta} \\\\ V &= -A_y = -P\sin{\theta} \\\\ M &= -M_A + A_ya = -PL\sin{\theta} + P\sin{\theta}a = -P\sin{\theta}(L-a) \end{align}
수직력에 의한 수직 응력은 다음과 같이 결정된다. 음수가 나오므로 이 외팔보는 압축(compression) 상태에 있다.
$$ \sigma_x = \frac{F}{A} = -\frac{P}{A}\cos{\theta} $$
전단력에 의한 전단 응력은 다음과 같이 결정된다. 음수가 나오므로 그림 7에 나타낸 전단력의 방향 $V$와 반대 방향으로 작용한다.
$$ \tau_{xy} = \frac{V}{A} = -\frac{P}{A}\sin{\theta} $$
굽힘 모멘트 $M$에 의해 발생하는 수직 응력이 있지만 지금은 다루지 않기로 한다. Beam 부재를 굽힐 때 굽힘 모멘트에 의한 전단 응력 역시 발생하지만 부재가 가늘고 길다면 오일러 빔(Euler beam)으로 취급하여 굽힘에 의한 전단 응력은 발생하지 않는다고 가정한다. 이것 또한 추후에 beam의 처짐(deflection)을 공부하고 난 뒤에 다루기로 한다. 앞으로 공부할 내용이 흥미진진죠?
4. 응력 텐서 (Stress Tensor)
텐서(tensor)는 불변량(invariant)이 존재하는 물리량을 말한다. 여기에서 불변량은 좌표를 변환해도 값이 변하지 않는 물리량을 의미한다. 대표적으로 질량은 좌표를 아무리 돌려서 어느 시점에서 보아도 같은 물리량이다. 질량처럼 방향이 없는 물리량을 스칼라(scalar)라고 하고 0차 텐서라고 한다. 방향을 갖는 벡터(vector)는 1차 텐서, 2x2 행렬(matrix)은 2차 텐서가 된다. 그러나 3x3 이상부터는 그냥 텐서라고 부른다.
응력 성분도 행렬 표기를 하면 편리하기 때문에 아래와 같은 방법으로 자주 사용하게 된다.
$$ \begin{bmatrix} \sigma \end{bmatrix} = \begin{bmatrix} \sigma_{xx} & \sigma_{xy} & \sigma_{xz} \\ \sigma_{yx} & \sigma_{yy} & \sigma_{yz} \\ \sigma_{zx} & \sigma_{zy} & \sigma_{zz} \end{bmatrix} = \begin{bmatrix} \sigma_{x} & \tau_{xy} & \tau_{xz} \\ \tau_{yx} & \sigma_{y} & \tau_{yz} \\ \tau_{zx} & \tau_{zy} & \sigma_{z} \end{bmatrix} $$




최근댓글