트러스 구조물의 변형 (Deformation of Truss Structure)
1. 트러스 (Truss)
트러스는 단축 부재로 이루어진 삼각형 구조물이다. 모두가 알고 있는 대표적인 트러스 구조물은 에펠탑이다. 실제로 에펠탑에 처음 트러스 구조가 쓰였다고 한다. 사실 에펠탑은 엑스포에서 기술력을 자랑할 목적으로 만든 전시품이었다. 당시에는 트러스 구조를 이용해 세계에서 가장 높은 구조물을 만들고 20년 후에 철거할 예정이었다. 처음에는 아름다운 파리에 거대한 쇳덩이가 생긴다고 여론이 좋지 않았다는 것 같다. 그런데 이게 생각보다 인기가 좋기도 하고 파리에서 가장 높은 구조물이어다보니 라디오나 TV 송신탑으로 쓰기 좋아서 살아남았다. 실제로 가서 봤을 때는 우리 집 뒷산에 있는 송전탑같이 생겨서 별 감흥이 없었는데 사실 의미가 큰 탑이었다.

2. 회전을 고려하지 않는 변형
2.1. 단순 트러스 (Simple Truss)
단순 트러스는 그림 2처럼 삼각형 딱 하나만 있는 트러스 구조물을 말한다. 트러스 구조물의 변형을 계산하는 방법을 단순 트러스를 이용해 알아보자. 아래 그림 2에서 B점의 변위를 구해본다.
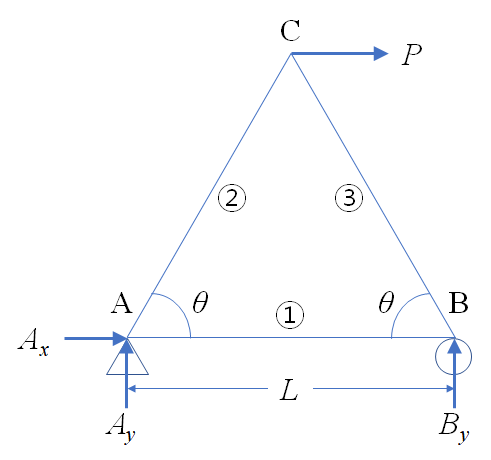
반력은 다음과 같이 전체 구조물의 평형 방정식을 통해 구한다.
\begin{align} \sum F_x &= A_x + P = 0 \\\\ \sum F_y &= A_y + B_y = 0 \\\\ \sum M_z|_A &= B_y\frac{L}{2} - PL\tan\theta = 0 \end{align}
B점을 절단해 평형 방정식을 통해 내력 $F_1$을 구한다.
\begin{align} \sum F_x &= -F_1 - F_3\cos\theta = 0 \\\\ \sum F_y &= F_3\sin\theta + B_y =0 \end{align}
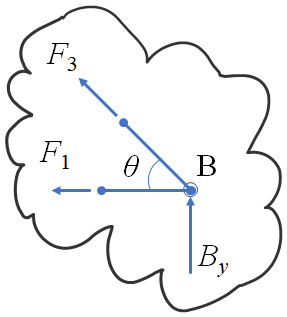
A점은 x 방향으로 고정되어 있고 B점은 x방향으로만 움직일 수 있기 때문에 B점의 변위는 1번 부재의 축방향 변형량과 같다.
$$ \Delta_B = \Delta_1 = \frac{F_1L}{E_1A_1} $$
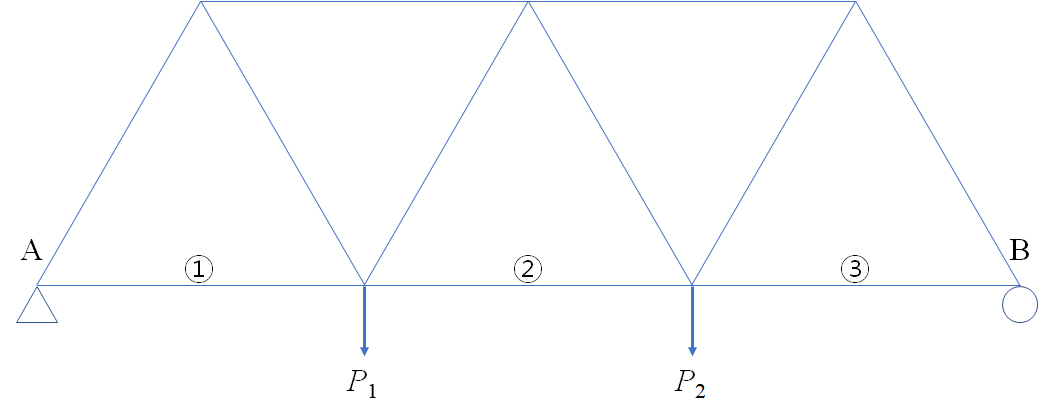
2.2. 단순하지 않은 트러스
아래 그림 4와 같은 트러스 구조물에서 B점의 변위를 구하는 방법은 단순 트러스와 동일하다. 각 부재의 내력을 구한 뒤 1번, 2번, 3번 부재의 변형을 더하면 B점의 변위가 된다. 실제로는 부재와 부재가 만나는 절점에서 회전이 있겠지만 회전이 아주 작다면 거의 비슷한 값을 얻게 될 것이다.
$$ \Delta_1 = \frac{F_1L_1}{E_1A_1},\quad \Delta_2 = \frac{F_2L_2}{E_2A_2},\quad \Delta_3 = \frac{F_3L_3}{E_3A_3} $$
$$ \Delta_B = \Delta_1 + \Delta_2 + \Delta_3 $$
3. 회전을 고려한 변형
지금까지는 부재의 축방향 변형량이 구하고자 하는 위치의 변위와 같아서 답을 쉽게 구할 수 있었다. 이제 아래 그림 5와 같은 크레인 구조물을 생각해보자. 이 구조물은 지지 조건이 모두 핀(pin)이기 때문에 회전을 무시할 수 없고 C점은 x방향뿐만 아니라 y방향으로도 움직이게 된다. 이 구조물의 부재 1은 영률 $E_1$, 단면적 $A_1$, 그리고 길이 $L_1 = L/\tan\theta$을 갖고 부재 2는 영률 $E_2$, 단면적 $A_2$, 그리고 길이 $L_2 = L/\sin\theta$를 갖는다.
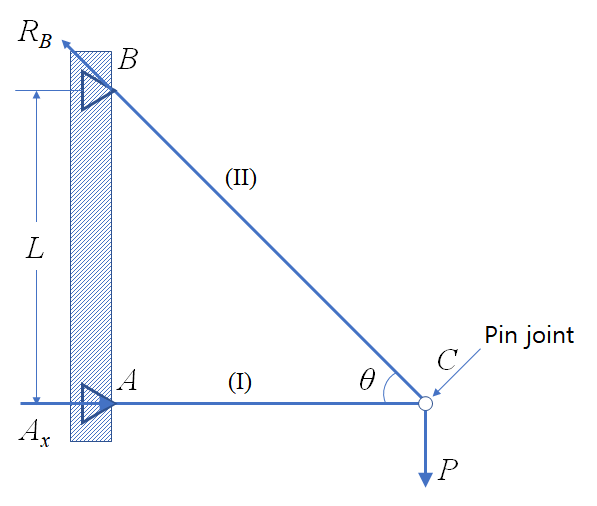
반력은 아래와 같이 전체 구조물의 평형 방정식을 통해 구하고 C점 부근에서 분할법을 이용해 내력을 구할 수 있다. 지난 글에서 많이 다뤘으니 과정은 생략한다.
\begin{align} F_1 &= -A_x = -\frac{P}{\tan\theta} \\\\ F_2 &= R_B = \frac{P}{\sin\theta} \end{align}
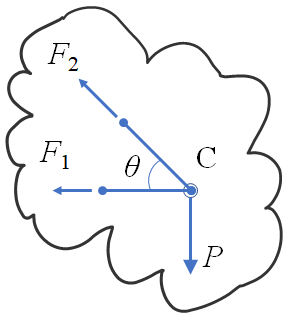
각 부재의 변형은 다음과 같다.
\begin{align} \Delta_1 &= \frac{F_1L_1}{E_1A_1} \\\\ \Delta_2 &= \frac{F_2L_2}{E_2A_2} \end{align}
3.1. 실제 구조물의 변형
실제 구조물의 변형은 아래 그림 7과 같을 것이다. 부재 1은 길이가 변형되어 $L_1 + \Delta_1$ 반경을 갖고 A점을 기준으로 회전하고 부재 2는 $L_2 + \Delta_2$의 반경을 갖고 B점을 기준으로 회전한다. 따라서 두 부재의 끝단 C점이 그리는 원의 교점이 C점의 변형 후 최종 위치가 될 것이다. 내력을 구해보면 부재 1은 압축 상태가 되지만 $\Delta_1$을 양수로 취급하여 늘어나는 방향으로 그렸다. 부재의 인장과 압축은 하중 $P$의 방향에 따라 달라질 것이다.
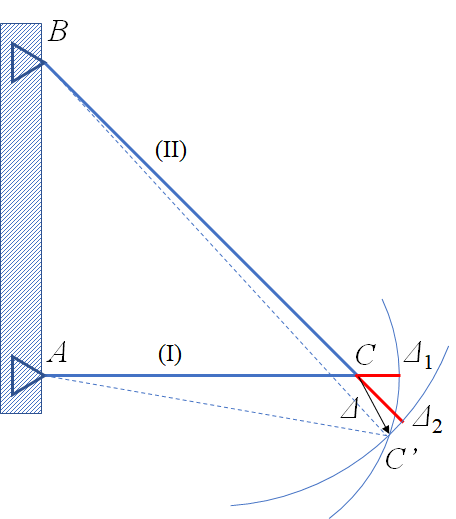
부재의 초기 길이는 기하에 의해 아래와 같다.
\begin{align} L_1 &= \frac{L}{\tan\theta} \\\\ L_2 &= \frac{L}{\sin\theta} \end{align}
변형 후의 부재 길이는 각 부재의 회전 반경이 된다.
\begin{align} R_1 &= L_1 + \Delta_1 \\\\ R_2 &= L_2 + \Delta_2 \end{align}
변형 후 각 부재가 그리는 원의 방정식은 교점 C(x_c, y_c)를 지난다.
\begin{align} x_c^2 + y_c^2 = R_1^2 \\\\ x_c^2 + (y_c - L)^2 = R_2^2 \end{align}
위의 두 원의 방정식의 교점을 구해보자.
$$ y_c^2 - (y_c - L)^2 = R_1^2 - R_2^2 $$
정리하면,
$$ 2Ly_c - L^2 = R_1^2 - R_2^2 $$
따라서 교점 C는 다음과 같다. x 좌표는 양의 근이 될 것이다.
\begin{align} \therefore y_c &= \frac{R_1^2 - R_2^2 + L^2}{2L} \\\\ x_c &= \pm\sqrt{R_1^2 - y_c^2} \end{align}
C 점의 총변위는 다음과 같이 피라고라스의 정리를 이용해 구한다.
$$ \Delta = \sqrt{(x_c - L_1)^2 + y_c^2} $$
3.2. Williot Method
위처럼 단순한 구조물의 변형을 구하는 것도 간단하지 않은데 복잡한 구조물은 더욱 어렵게 된다. 요즘이야 뛰어난 성능의 컴퓨터와 상용 유한요소해석 소프트웨어를 쉽게 사용할 수 있지만 불과 수십 년 전에만 해도 손으로 계산하는 것이 더 빨랐다. Williot method는 프랑스 아저씨가 트러스 구조물의 변형을 근사치로 계산하는 방법을 제안한 것으로 변형이 크지 않다면 실제 해와 거의 유사한 결과를 준다. 살짝 회전하는 정도는 원의 방정식을 쓰지 말고 그냥 직각 삼각형으로 대충 그려서 계산하면 된다는 것이다. 그림 7에서는 변형량을 크게 그렸기 때문에 부재가 회전하는 자취가 곡률을 갖는다. 그러나 변형이 아주 작게 되면 곡률은 거의 눈에 띄지 않게 되어 그림 8처럼 직선으로 대충 그려도 얼추 맞을 것이다.

그림 8에서 각 부재에 늘어난 길이를 반영해서 연장한다. 변형 이후의 끝점에 수직선을 긋고 두 수직선이 만나는 점을 최종 변형 위치로 한다. 각 부재의 변형량은 다음 관계를 갖는다.
\begin{align} \theta_2 &= \theta - \theta_1 \\\\ \Delta_1 &= \Delta\cos\theta_1 \\\\ \Delta_2 &= \Delta\cos\theta_2 \end{align}
$$ \therefore \Delta = \frac{\Delta_1}{\cos\theta_1} = \frac{\Delta_2}{\cos\theta_2} $$
위 식에서 변형량 $\Delta_1$과 $\Delta_2$의 비율을 구할 수 있다.
$$ \frac{\cos\theta_2}{\cos\theta_1} = \frac{\Delta_2}{\Delta_1} $$
다시 첫 번째 각도에 대한 식을 $\cos$ 함수에 대입하고 삼각함수의 합차 공식을 이용해 전개한다.
\begin{align} \theta_2 &= \theta_1 - \theta \\\\ \cos\theta_2 &= \cos(\theta_1-\theta) \\\\ &= \cos\theta_1\cos\theta +\sin\theta_1\sin\theta \end{align}
위 식의 양변을 $\cos\theta_1$으로 나눈다.
$$ \frac{\cos\theta_2}{\cos\theta_1} = \cos\theta + \tan\theta_1\sin\theta $$
$$ \therefore \frac{\Delta_2}{\Delta_1} = \cos\theta + \tan\theta_1\sin\theta $$
따라서 각도 $\theta_1$은 다음과 같이 결정된다.
$$ \theta_1 = \tan^{-1}\left[\frac{1}{\sin\theta}\left(\frac{\Delta_2}{\Delta_1}-\cos\theta\right)\right] $$
최종 변형은 위에서 구한 각도를 다시 처음 식에 대입해서 구할 수 있다.
$$ \Delta = \frac{\Delta_1}{\cos\theta_1} $$
길이 $L=1\text{m}$이고 각도 $\theta=45^\circ$인 구조에 직경 $d=10 \text{cm}$, 영률 $E=70 \text{GPa}$인 부재를 이용하고 작용하는 하중이 $P=100\text{N}$인 경우 엄밀하게 구한 해는 $\Delta = 7.19721e-7 \text{m}$가 된다. Williot method를 이용할 경우에도 거의 동일한 결과를 얻을 수 있다. 아래 그림 9에 정확한 해와 근사해를 비교했다. 하중에 증가함에 Williot method의 오차가 얼마나 커지는 지를 알 수 있다. 이 그래프는 가로 축이 로그 스케일이다.
결과를 보면 하중이 1백만 N이 될 때까지 오차는 2%를 넘지 않는다. 하중이 1백만 N이라는 것은 약 100 톤의 하중이 걸리는 것인데 이 정도 구조물에 100 톤을 쓸리는 없으니 실제로 쓰일 작은 하중 조건 또는 작은 변형에서는 거의 오차가 없는 셈이다. 오차가 커지는 경우는 부재의 원래 길이에 필적할만한 변형이 있는 경우가 되니 이것은 애초에 물리적으로 가능할 것 같지 않다.
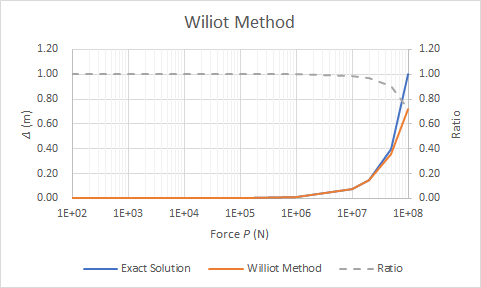
3.3 Williot Method 예제
그림 10과 같은 구조물에서 하중점의 변형을 Williot method로 구해보자
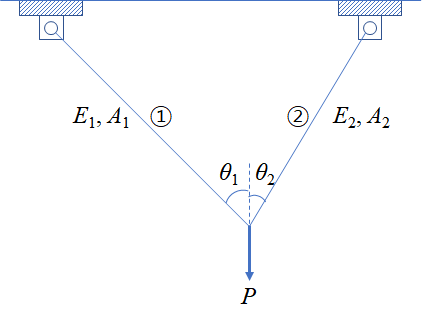
반력을 구한 뒤 내력을 결정해도 되지만 하중점에서 분할법을 이용해 직접 내력을 구할 수도 있다.
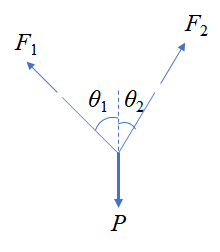
\begin{align} \sum F_x &= -F_1\sin\theta_1 + F_2\sin\theta_2 = 0 \\\\ \sum F_y &= F_1\cos\theta_1 + F_2\cos\theta_2 - P = 0 \end{align}
위 평형 방정식을 풀어 내력 $F_1,\ F_2$를 구하고 부재의 변형 $\Delta_1, \Delta_2$를 구한다.
하중점에서 Williot diagram을 그려보면 아래와 같다.
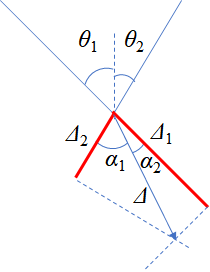
엇각을 이용해 각도에 대한 식을 쓰고 $\cos$ 합차 공식으로 전개한다.
\begin{align} \alpha_2 &= \theta_1 + \theta_2 - \alpha_1 \\\\ \Delta_1 &= \Delta\cos\alpha_1 \\\\ \Delta_2 &= \Delta\cos\alpha_2 \end{align}
$$ \therefore \Delta = \frac{\Delta_1}{\cos\alpha_1} = \frac{\Delta_2}{\cos\alpha_2} $$
\begin{align} \cos\alpha_2 &= \cos(\theta_1+\theta_2)\cos\alpha_1 + \sin(\theta_1+\theta_2)\tan\alpha_1 \\\\ \frac{\Delta_2}{\Delta_1} &= \cos(\theta_1+\theta_2)\cos\alpha_1 + \sin(\theta_1+\theta_2)\tan\alpha_1\end{align}
$$ \therefore \alpha_1 = \tan^{-1}\left[\frac{1}{\sin(\theta_1+\theta_2)}\left(\frac{\Delta_2}{\Delta_1}-\cos(\theta_1+\theta_2\right)\right] $$
따라서 하중점의 변형은 다음과 같다.
$$ \therefore \Delta = \frac{\Delta_1}{\cos\alpha_1} $$